
 如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,AB=AD+BC.求证:BE⊥AE.
如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,AB=AD+BC.求证:BE⊥AE. 分析 由题意,延长AE、BC交于点F,由AD∥BC,得∠DAE=∠CFE,然后,通过证明△ADE≌△CFE,由AB=BC+AD=BC+FC=BF得出△ABF为等腰三角形,根据等腰三角形的三线合一,即可证得.
解答 解:如图,延长AE、BC交于点F,
∵AD∥BC,
∴∠DAE=∠CFE,
∠ECF=∠EDA
∵点E是CD的边中点,
∴DE=CE,
∴△ECF≌△EDA(AAS),
∴AD=FC,AE=FE
∵AB=BC+AD,BF=BC+FC
∴AB=BF
即三角形ABF为等腰三角形,又AE=FE
故由等腰三角形三线合一得AF⊥BE
∴BE⊥AE.
点评 本题主要考查了全等三角形的判定与性质及等腰三角形的性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.


科目:初中数学 来源: 题型:选择题
| A. | 若x=y,则x-5=y-5 | B. | 若a=b,则ac=bc | C. | 若x=y,则x+a=y+a | D. | 若x=y,则$\frac{x}{a}$=$\frac{y}{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,把一张矩形的纸片沿图中的虚线裁成三张大小相同的小矩形纸片.若得到的小矩形纸片与原来大矩形纸片相似,则大矩形纸片的长与宽的比值为$\sqrt{3}$.
如图,把一张矩形的纸片沿图中的虚线裁成三张大小相同的小矩形纸片.若得到的小矩形纸片与原来大矩形纸片相似,则大矩形纸片的长与宽的比值为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -6、1 | B. | 6、1 | C. | 6、-1 | D. | -6、-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x=70%×84 | B. | x=(1+70%)×84 | C. | 84=70%x | D. | 84=(1-70%)x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
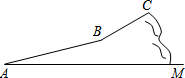 今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.
今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com