练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．已知a+b=3，ab=1，求代数式$\sqrt{\frac{2a}{b}}+\sqrt{\frac{2b}{a}}$=3$\sqrt{2}$．

    分析 利用已知ab之间的关系进而化简二次根式，求出即可．

    解答 解：∵a+b=3，ab=1，
    ∴$\sqrt{\frac{2a}{b}}+\sqrt{\frac{2b}{a}}$=$\frac{\sqrt{2ab}}{b}$+$\frac{\sqrt{2ab}}{a}$=$\frac{\sqrt{2}}{b}$+$\frac{\sqrt{2}}{a}$=$\frac{\sqrt{2}（a+b）}{ab}$=3$\sqrt{2}$．
    故答案为：3$\sqrt{2}$．

    点评 此题主要考查了二次根式的化简求值，正确应用已知条件化简是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．一部电梯最大负荷为1000kg，有12人携带40kg的东西乘电梯，他们的平均体重x应该满足什么条件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．下列格式由左到右的变形，正确的是①④（填写序号）
    ①-a+b=-（a-b）
    ②（x-y）2=-（y-x）2
    ③（a-b）3=（b-a）3
    ④（x-1）（y-1）=（1-x）（1-y）
    ⑤（-a-b）2=-（a-b）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

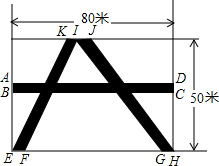    17．如图，有一块长为80米，宽为50米得长方形绿地，其中有三条笔直的道路（图中的阴影部分、道路的一边AD与长方形绿地的一边平行，且道路的出入口的边AB、CD、EF、GH、KI、IJ的长度都相同），其余的部分种植绿化，已知道路面积为352平方米，求道路出入口的边的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

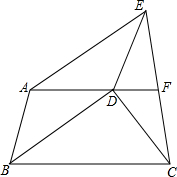    4．A、D、F在同一直线上，F是CE的中点，EC⊥BC、BA∥DE，BD∥AE．甲、乙两人同时从住所B地步行到F地办公，若甲走的路线是B-A-E-F；乙走的路线是B-D-C-F，假设两人行走的速度相同，那么谁先到达办公地点F？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，在平面直角坐标系中，矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上，OA=8，OC=4．点P从点O出发，沿x轴以每秒2个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D，点D随点P的运动而运动，连接DP、DA．
    （1）填空：当t=3时，点D恰好落在AB上，即△DPA成为直角三角形；
    （2）若以点D为圆心，DP为半径的圆与CB相切，求t的值；
    （3）在点P从O向A运动的过程中，△DPA能否成为等腰三角形？若能，求t的值；若不能，请说明理由；
    （4）填空：在点P从点O向点A运动的过程中，点D运动路线的长为4$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

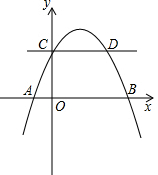    9．如图，已知：抛物线y=ax2+bx+2（a≠0）交x轴于A（-1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．
    （1）求抛物线解析式及点D坐标；
    （2）若点E在x轴上，且以A，E，D，P为顶点的四边形是平行四边形，求点P的坐标；
    （3）若点P在y轴右侧，过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．据电力部门统计，每天8：00至21：00是用电的高峰期，简称“峰时”，21：00至次日8：00是用电的低谷时期，简称“谷时”，为了缓解供电需求紧张矛盾，某市电力部门于本月初统一换装“峰谷分时”电表，对用电实行“峰谷分时电价”新政策，具体见下表：
    时间换表前换表后
    峰时（8：00～21：00）谷时（21：00～次日8：00）
    电价每度0.52元每度0.55元每度0.30元
    （1）小张家上月“峰时”用电50度，“谷时”用电20度，若上月初换表，则相对于换表前小张家的电费是增多了还是减少了？增多或减少了多少元？请说明理由．
    （2）小张家这个月用电95度，经测算比换表前使用95度电节省了5.9元，问小张家这个月使用“峰时电”和“谷时电”分别是多少度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列运算正确的是（　　）
    A．-（-2）2=-4B．（-3）2=6C．-|-3|=3D．（-3）2=-2

    查看答案和解析>>

    同步练习册答案