
分析 把已知等式两边除以x可得到x-$\frac{1}{x}$=4,再利用完全平方公式变形得到x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2,然后利用整体代入的方法计算,然后把$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$变形为$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$,然后利用整体代入的方法.
解答 解:∵x2-4x-1=0,
∴x-4-$\frac{1}{x}$=0,
∴x-$\frac{1}{x}$=4,
x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2=16+2=18,
$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$=$\frac{1}{18+1}$=$\frac{1}{19}$.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.


科目:初中数学 来源: 题型:填空题
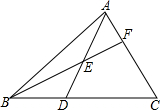 在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.
在△ABC中,D在BC上,E在AD上,连结BE,并延长交AC于F,若3BD=2CD,AE=DE,则$\frac{AF}{FC}$=$\frac{2}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
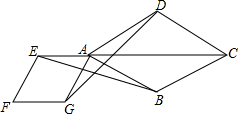 如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且∠EAG=∠BAD,连接EC,CD.
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且∠EAG=∠BAD,连接EC,CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.5×103 | B. | 4.5×104 | C. | 4.5×105 | D. | 0.45×105 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com