
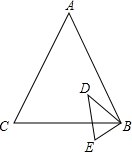
 如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$.
如图,已知在△ABC和△EBD中,$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$.分析 (1)根据已知条件得到△ABC∽△DBE,根据相似三角形的性质:相似三角形周长的比等于相似比即可得到结论;
(2)根据已知条件得到△ABC∽△DBE,根据相似三角形的性质:相似三角形面积的比等于相似比的平方即可得到结论;
解答 解:(1)∵$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$,
∴△ABC∽△DBE,
∴△ABC的周长:△EBD的周长=$\frac{5}{2}$,
设△ABC的周长为5k,△EBD的周长为2k,
∴5k-2k=60,
∴k=20,
∴△ABC的周长=100cm,△EBD的周长=40cm;
(2)∵$\frac{AB}{EB}=\frac{BC}{BD}=\frac{AC}{ED}=\frac{5}{2}$,
∴△ABC∽△DBE,
∴$\frac{{S}_{△ABC}}{{S}_{△DBE}}$=($\frac{5}{2}$)2=$\frac{25}{4}$,
∵△ABC与△EBD的面积之和为812cm2,
∴S△ABC=812×$\frac{25}{29}$=700,
S△EBD=812×$\frac{4}{29}$=112.
点评 本题考查了相似三角形的判定和性质,三角形的面积和周长,熟练掌握相似三角形的判定和性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
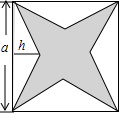 如图,一个正方形剪去四个相同的三角形,已知正方形的边长为a,三角形的高为h
如图,一个正方形剪去四个相同的三角形,已知正方形的边长为a,三角形的高为h查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
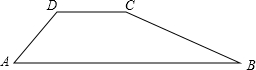 如图,某一大坝的横截面是四边形ABCD.其中AB∥DC,坝顶宽CD=3m,坝高6m,迎水坡BC的坡度i1=1:2.背水坡AD的坡度i2=1:1,求斜坡AD坡角∠A和坝底宽AB.
如图,某一大坝的横截面是四边形ABCD.其中AB∥DC,坝顶宽CD=3m,坝高6m,迎水坡BC的坡度i1=1:2.背水坡AD的坡度i2=1:1,求斜坡AD坡角∠A和坝底宽AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com