考点:相似多边形的性质,一次函数图象上点的坐标特征
专题:规律型
分析:根据直线解析式求出点OA1,得到第一个正方形的边长,根据点B3的坐标求出第三个正方形的边长以及A3的坐标,然后求出第二个正方形的边长,再表示出A2B1、A3B2,然后求出△A1A2B1和△A2A3B2相似,根据相似三角形对应边成比例列式求b,再把点A3的坐标代入直线求出k,然后代入代数式进行计算即可得解.
解答:解:令x=0,则y=b,
所以,OA
1=b,
∵点B
3的坐标是(
,
),
∴第三个正方形的边长A
3C
2=
,A
3(
,
),
∴第二个正方形的边长为
-b,
∴A
2B
1=
-2b,A
3B
2=
-(
-b)=b-
,
∵正方形A
1B
1C
1D
1,A
2B
2C
2D
2,A
3B
3C
3D
3是彼此相似的多边形,
∴点B
3的坐标是(
,
),
∴△A
1A
2B
1∽△A
2A
3B
2,
∴
=
,
∴
=
,
整理得,4b
2-29b+25=0,
解得b
1=1,b
2=
(舍去),
所以,直线解析式为y=kx+1,
把A
3(
,
)代入得,
k+1=
,
解得k=
,
所以5k-bk=5×
-1×
=2.
点评:本题考查了相似多边形的性质,一次函数图象上点的坐标特征,用b表示出正方形的边长,然后利用相似三角形对应边成比例列式求出b是解题的关键,也是本题的难点.

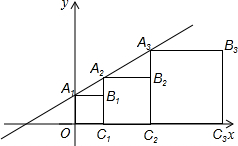 彼此相似的正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是(
彼此相似的正方形A1B1C1D1,A2B2C2D2,A3B3C3D3,点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是(

