
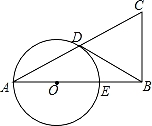
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC•AD=AB•AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
【考点】切线的性质;相似三角形的判定与性质.
【分析】(1)连接DE,根据圆周角定理求得∠ADE=90°,得出∠ADE=∠ABC,进而证得△ADE∽△ABC,根据相似三角形对应边成比例即可求得结论;
(2)连接OD,根据切线的性质求得OD⊥BD,在RT△OBD中,根据已知求得∠OBD=30°,进而求得∠BAC=30°,根据30°的直角三角形的性质即可求得AC的长.
【解答】(1)证明:连接DE,
∵AE是直径,
∴∠ADE=90°,
∴∠ADE=∠ABC,
∵∠DAE=∠BAC,
∴△ADE∽△ABC,
∴ =
=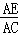 ,
,
∴AC•AD=AB•AE;
(2)解:连接OD,
∵BD是⊙O的切线,
∴OD⊥BD,
在RT△OBD中,OE=BE=OD,
∴OB=2OD,
∴∠OBD=30°,
同理∠BAC=30°,
在RT△ABC中,AC=2BC=2×2=4.
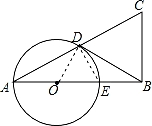
【点评】本题考查了圆周角定理的应用,三角形相似的判定和性质,切线的性质,30°的直角三角形的性质等,作出辅助线构建直角三角形是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
.如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的边长为( )
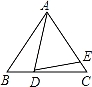
A.9 B.12 C.15 D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:如图所示,点P, Q分别代表两个小区,直线l代表临近小区的一条公路.点P到直线l的距离为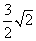 千米,两点P、Q所在直线与直线l的夹角为45°,两小区P、Q之间的距离为1千米.根据居民出行的需要,计划在公路l上的某处设置一个公交车站.考虑到修路的费用问题,希望车站的位置到小区P和小区Q的距离之和m最短,请在公路l上画出车站的位置(用点M表示,保留画图痕迹,不写作法),并求出m的值.
千米,两点P、Q所在直线与直线l的夹角为45°,两小区P、Q之间的距离为1千米.根据居民出行的需要,计划在公路l上的某处设置一个公交车站.考虑到修路的费用问题,希望车站的位置到小区P和小区Q的距离之和m最短,请在公路l上画出车站的位置(用点M表示,保留画图痕迹,不写作法),并求出m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com