
某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件.若使利润最大,每件的售价应为 元.
科目:初中数学 来源: 题型:
若点(x1,y1),(x2,y2),(x3,y3)都是反比例函数y=﹣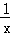 图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
图象上的点,并且y1<0<y2<y3,则下列各式中正确的是( )
A.x1<x2<x3 B.x1<x3<x2 C.x2<x1<x3 D.x2<x3<x1
查看答案和解析>>
科目:初中数学 来源: 题型:
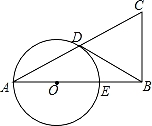
已知在△ABC中,∠B=90°,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC•AD=AB•AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
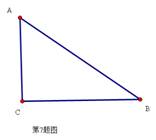
如图,在Rt∆ABC中,∠C=90°, ∠B = 30°,BC = 4cm,以点C为圆心,以2cm长为半径作圆,⊙C与AB的位置关系是( )
A.相离  B.相切 C.相交 D.相交或相切
B.相切 C.相交 D.相交或相切
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com