【题目】给出下列四个结论，其中正确的结论为（ ）
A. 等边三角形既是轴对称图形，又是中心对称图形
B. 对角线相等的四边形是矩形
C. 三角形的外心到三个顶点的距离相等
D. 任意三个点都可确定一个圆
科目：初中数学 来源： 题型：
【题目】小明想了解全校3000名同学对新闻、体育、音乐、娱乐、戏曲五类电视节目的喜爱况，从中抽取了一部分同学进行了一次抽样调查，利用所得数据绘制成下面的统计图：根据图中所给信息，全校喜欢娱乐类节目的学生大约有（ ）人．
A. 1080 B. 900 C. 600 D. 108
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】太平商场销售一批名牌
恤，平均每天可售出
件，每件盈利
元，为了扩大销售，增加盈利，商场决定采用适当的降价措施，经调查，如果每件恤每降价
元，商场平均每天多售出
件，
①若商场平均每天要盈利
元，则每件恤应降价多少元？
②每件恤降价多少元时，商场平均每天盈利最多？最大盈利多少元？请说明你的理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（8分）如图，⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F．
（1）若∠E=∠F时，求证：∠ADC=∠ABC；
（2）若∠E=∠F=42°时，求∠A的度数；
（3）若∠E=α，∠F=β，且α≠β．请你用含有α、β的代数式表示∠A的大小．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图像与
轴交于点
，与
轴交于点
，且经过点
．
(1)当
时；
①求一次函数的表达式；
②
平分
交轴于点
，求点的坐标；
(2)若△
为等腰三角形，求
的值；
(3)若直线
也经过点
，且
，求的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD 是△ABC 的角平分线，DE，DF 分别是△BAD 和△ACD 的高，得到下列四个结论：①OA＝OD；②AD⊥EF；③当∠A＝90°时，四边形 AEDF 是正方形；④AE+DF＝AF+DE．其中正确的是_________（填序号）．
查看答案和解析>>
科目：初中数学 来源： 题型：
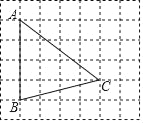
【题目】如图，在每个小正方形的边长为1的网格中，点A，B，C均在格点上．
（Ⅰ）AC的长等于_____；
（Ⅱ）在线段AC上有一点D，满足AB2=ADAC，请在如图所示的网格中，用无刻度的直尺，画出点D，并简要说明点D的位置是如何找到的（不要求证明）_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在同一平面直角坐标系中画出函数
和
的图象．
观察图象，说出抛物线的顶点坐标、开口方向、对称轴；
说出各函数的最值；
说明各函数图象在对称轴两侧部分的函数值
随
的增大而变化的情况．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列分解因式的过程：x2＋2xy－3y2
解：原式＝x2＋2xy＋y2－y2－3y2
＝(x2＋2xy＋y2)－4y2
＝(x＋y)2－(2y)2
＝(x＋y＋2y)(x＋y－2y)
＝(x＋3y)(x－y)
像这种通过增减项把多项式转化成完全平方形式的方法称为配方法.
（1）请你运用上述配方法分解因式：x2＋4xy－5y2
（2）代数式x2＋2x＋y2－6y＋15是否存在最小值？如果存在，请求出当x、y分别是多少时，此代数式存在最小值，最小值是多少？如果不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
