
 ��ͼ��ֱ������ϵ�У���A������Ϊ��1��0�������߶�OAΪ���ڵ������������ȱߡ�AOB����CΪx��������һ���㣨OC��1��������BC�����߶�BCΪ���ڵ������������ȱߡ�CBD��ֱ��DA��y���ڵ�E��
��ͼ��ֱ������ϵ�У���A������Ϊ��1��0�������߶�OAΪ���ڵ������������ȱߡ�AOB����CΪx��������һ���㣨OC��1��������BC�����߶�BCΪ���ڵ������������ȱߡ�CBD��ֱ��DA��y���ڵ�E������ ��1���жϡ�OBC���ABDȫ�ȣ��ɵȱߡ�AOB�͵ȱߡ�CBD�õ�ȫ��������
��2����P��0��m�����ӳ�AB��y����F����Rt��OAF�У���OA=1����AFO=30�㣬�Ƴ�OF=$\sqrt{3}$OA=$\sqrt{3}$������S��PAB=S��PAF-S��PBF���ɵ�2=$\frac{1}{2}$��m+$\sqrt{3}$��•1-$\frac{1}{2}$��m+$\sqrt{3}$��•$\frac{1}{2}$���ⷽ�����m�����ɽ�����⣮
��3�����ݣ�1�����õ���OAE=60�㣬Ȼ�����и���ֱ��������30�㣬���Ե�ֱ�DZߵ���б�ߵ�һ����Եõ�AE=2���Ӷ��õ�E�������ǹ̶��ģ�
��� �⣺��1����OBC�ա�ABD��
���ɣ��ߡ�AOB�ǵȱ������Σ�
��OB=AB����OBA=��OAB=60�㣬
�֡ߡ�CBD�ǵȱ�������
��BC=BD����CBD=60�㣬
���OBA+��ABC=��CBD+��ABC��
����OBC=��ABD��
�ڡ�OBC�͡�ABD�У�
$\left\{\begin{array}{l}{OB=AB}\\{��OBC=��ABD}\\{BC=BD}\end{array}\right.$��
���OBC�ա�ABD��SAS����
��2����P��0��m�����ӳ�AB��y����F��
��Rt��OAF�У���OA=1����AFO=30�㣬
��OF=$\sqrt{3}$OA=$\sqrt{3}$��
��S��PAB=S��PAF-S��PBF��
��2=$\frac{1}{2}$��m+$\sqrt{3}$��•1-$\frac{1}{2}$��m+$\sqrt{3}$��•$\frac{1}{2}$��
��m=8-$\sqrt{3}$��
���P������0��8-$\sqrt{3}$����
���ݶԳ��ԣ�P���ڵ�F�ĶԳƵ�P��Ҳ����������P�䣨0��-8-$\sqrt{3}$����
�������������������ĵ�P����Ϊ��0��8-$\sqrt{3}$����0��-8-$\sqrt{3}$����
��3���ߡ�OBC�ա�ABD��
�ߡ�BAD=��BOC=60�㣬
�֡ߡ�OAB=60�㣬
���OAE=180��-��OAB-��BAD=60�㣬
��Rt��OEA��
�ߡ�OAE=60�㣬
���AEO=30�㣬
��AE=2OA=2��
��OE=$\sqrt{{2}^{2}-{1}^{1}}$=$\sqrt{3}$��
���E��λ�ò��ᷢ���仯��E������ΪE��0��$\sqrt{3}$����
���� ���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ������ε���������ɶ�����֪ʶ������Ĺؼ�����ȷѰ��ȫ�������Σ�ѧ�����÷ָ�������������ѧ���÷��̵�˼��˼�����⣬�����п�ѹ���⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
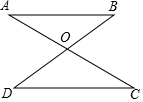 ��ͼ����֪AB��CD����֤����AOB�ա�COD���ɲ�������AB=CD��OA=OC��OB=OD������дһ���ʺϵ��������ɣ�
��ͼ����֪AB��CD����֤����AOB�ա�COD���ɲ�������AB=CD��OA=OC��OB=OD������дһ���ʺϵ��������ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
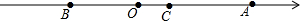 ��ͼ����������ԭ��O��ʾ������0��B���ʾ������m��A��ʾ������n���ң�m+4��2+|n-8|=0��
��ͼ����������ԭ��O��ʾ������0��B���ʾ������m��A��ʾ������n���ң�m+4��2+|n-8|=0���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���OA0A1����OA1A2����OA2A3����OA3A4�����ǵ���ֱ�������Σ���A0��1��0����A1��1��1����A2��0��2����A3��-2��2����A4��-4��0������������ͼ����ʾ���ɣ�A2015������Ϊ��21007��21007����
��ͼ����ƽ��ֱ������ϵ�У���OA0A1����OA1A2����OA2A3����OA3A4�����ǵ���ֱ�������Σ���A0��1��0����A1��1��1����A2��0��2����A3��-2��2����A4��-4��0������������ͼ����ʾ���ɣ�A2015������Ϊ��21007��21007�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-1 | B�� | x��2 | C�� | x�١�1 | D�� | x��-1��x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | C�� | 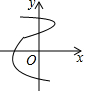 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ�����ľ���ֵ�������������������һ�������� | |
| B�� | û����С����������Ҳû�о���ֵ��С�������� | |
| C�� | �������ľ���ֵһ�������� | |
| D�� | ���|a|=-a����ôa��0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com