
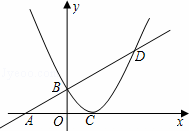
如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次函数y=ax2+bx+c的图象交于y轴上的一点B,二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2.
(1)求二次函数y=ax2+bx+c的解析式;
(2)设一次函数y=0.5x+2的图象与二次函数y=ax2+bx+c的图象的另一交点为D,已知P为x轴上的一个动点,且△PBD为直角三角形,求点P的坐标.
|
解答:解:(1)∵y=0.5x+2交x轴于点A, ∴0=0.5x+2, ∴x=-4,与y轴交于点B, ∵x=0, ∴y=2 ∴B点坐标为:(0,2), ∴A(-4,0),B(0,2), ∵二次函数y=ax2+bx+c的图象与x轴只有唯一的交点C,且OC=2 ∴可设二次函数y=a(x-2)2, 把B(0,2)代入得:a=0.5 ∴二次函数的解析式:y=0.5x2-2x+2; (2)(Ⅰ)当B为直角顶点时,过B作BP1⊥AD交x轴于P1点由Rt△AOB∽Rt△BOP1∴ ∴ 得:OP1=1, ∴P1(1,0), (Ⅱ)作P2D⊥BD,连接BP2, 将y=0.5x+2与y=0.5x2-2x+2联立求出两函数交点坐标:D点坐标为:(5,4.5), 则AD= 当D为直角顶点时 ∵∠DAP2=∠BAO,∠BOA=∠ADP2, ∴△ABO∽△AP2D, ∴ 解得:AP2=11.25, 则OP2=11.25-4=7.25, 故P2点坐标为(7.25,0); (Ⅲ)当P为直角顶点时,过点D作DE⊥x轴于点E,设P3(a,0) 则由Rt△OBP3∽Rt△EP3D 得: ∴ ∵方程无解, ∴点P3不存在, ∴点P的坐标为:P1(1,0)和P2(7.25,0).
|


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
| a | x |
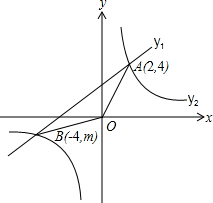 B(-4,m)两点.
B(-4,m)两点.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象与反比例函数y=-
如图,已知一次函数y=kx+b的图象与反比例函数y=-| 8 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•新疆)如图,已知一次函数y1=kx+b与反比例函数y2=
(2013•新疆)如图,已知一次函数y1=kx+b与反比例函数y2=| m | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数y=
如图,已知一次函数y=k1x+b经过A、B两点,将点A向上平移1个单位后刚好在反比例函数y=| k2 | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知一次函数y=kx+b的图象交反比例函数y=
如图,已知一次函数y=kx+b的图象交反比例函数y=| 4-2m |
| x |
| BC |
| AB |
| 1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com