
【题目】已知点I为△ABC的内心
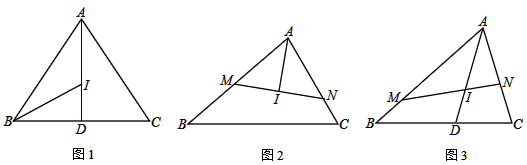
(1) 如图1,AI交BC于点D,若AB=AC=6,BC=4,求AI的长
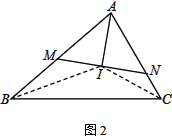
(2) 如图2,过点I作直线交AB于点M,交AC于点N
① 若MN⊥AI,求证:MI2=BM·CN
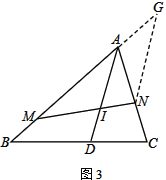
② 如图3,AI交BC于点D.若∠BAC=60°,AI=4,请直接写出![]() 的值
的值
【答案】(1)AI的长是![]() ;
;
(2)①证明见解析;② ![]()
【解析】试题分析:(1)、根据内心的性质得出AD为线段BC的中垂线,然后根据Rt△BID的勾股定理得出答案;(2)、首先得出△AMI和△ANI全等,从而得出∠AMN=∠ANM,然后连接BI和CI,根据角度之间的关系得出△BMI和△INC相似,则NI2=BM·CN,根据NI=MI得出答案;(3)、过点N作NG∥AD交MA的延长线于G,则∠ANG=∠AGN=30° ∴AN=AG,NG=![]() 然后根据平行线性质得出
然后根据平行线性质得出![]() ,然后代入得出答案.
,然后代入得出答案.
试题解析:(1) ![]()
(2) ∵I为△ABC的内心 AI⊥MN ∴△AMI≌△ANI(ASA) ∴∠AMN=∠ANM
连接BI、CI ∴∠BMI=∠CNI
设∠BAI=∠CAI=α,∠ACI=∠BCI=β ∴∠NIC=90°-α-β
∵∠ABC=180°-2α-2β ∴∠MBI=90°-α-β ∴△BMI∽△INC
∴![]() ∴NI2=BM·CN ∵NI=MI ∴MI2=BM·CN
∴NI2=BM·CN ∵NI=MI ∴MI2=BM·CN
(3) 过点N作NG∥AD交MA的延长线于G ∴∠ANG=∠AGN=30° ∴AN=AG,NG=![]()
∵AI∥NG ∴![]() ∴
∴![]() ,得
,得![]()


科目:初中数学 来源: 题型:
【题目】如图,已知线段AB=20,C是AB上的一点,D为CB上的一点,E为DB的中点,DE=3. ![]()
(1)若CE=8,求AC的长;
(2)若C是AB的中点,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题: 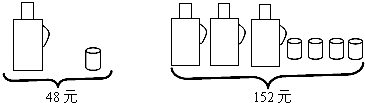
(1)一个水瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的水瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定:这两种商品都打八折;乙商场规定:买一个水瓶赠送两个水杯,另外购买的水杯按原价卖.若某单位想要买5个水瓶和20个水杯,请问选择哪家商场购买更合算,并说明理由.(必须在同一家购买)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年,国家统计局公布了第六次全国人口普查结果,总人口约为1339700000人,将1339700000用科学记数法表示正确的是( )
A.0.13397×1010
B.1.3397×109
C.13.397×108
D.13397×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“⊕”定义一种新运算:对于任意有理数a和b,规定a⊕b=ab2+2ab+a. 如:1⊕3=1×32+2×1×3+1=16.
(1)求(﹣2)⊕3的值;
(2)若( ![]() ⊕3)⊕(﹣
⊕3)⊕(﹣ ![]() )=8,求a的值.
)=8,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中与多项式2x﹣3y+4z相等的是( )
A.2x+(3y﹣4z)
B.2x﹣(3y﹣4z)
C.2x+(3y+4z)
D.2x﹣(3y+4z)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若AC=2, ![]() , 求菱形ABCD的面积.
, 求菱形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com