
【题目】在平面直角坐标系中,点A,B的坐标分别为(﹣3,0),(3,0),点P在反比例函数y=![]() 的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( )
的图象上,若△PAB为直角三角形,则满足条件的点P的个数为( )
A.2个
B.4个
C.5个
D.6个
【答案】D
【解析】①当∠PAB=90°时,P点的横坐标为﹣3, 把 x=﹣3 代入 y=![]() 得y=﹣
得y=﹣![]() , 所以此时P点有1个; ②当∠APB=90°, 设P(x,
, 所以此时P点有1个; ②当∠APB=90°, 设P(x,![]() ),PA2=(x+3)2+(
),PA2=(x+3)2+(![]() )2 , PB2=(x﹣3)2+(
)2 , PB2=(x﹣3)2+(![]() )2 , AB2=(3+3)2=36,因为PA2+PB2=AB2 , 所以(x+3)2+(
)2 , AB2=(3+3)2=36,因为PA2+PB2=AB2 , 所以(x+3)2+(![]() )2+(x﹣3)2+(
)2+(x﹣3)2+(![]() )2=36,整理得x4﹣9x2+4=0,所以x2=
)2=36,整理得x4﹣9x2+4=0,所以x2=![]() ,或x2=
,或x2=![]() ,所以此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,把x=3代入y=
,所以此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,把x=3代入y=![]() 得y=
得y=![]() ,所以此时P点有1个;综上所述,满足条件的P点有6个.故答案选:D.
,所以此时P点有1个;综上所述,满足条件的P点有6个.故答案选:D.
分类讨论:①当∠PAB=90°时,则P点的横坐标为﹣3,根据反比例函数图象上点的坐标特征易得P点有1个;②当∠APB=90°,设P(x,![]() ),根据两点间的距离公式和勾股定理得(x+3)2+(
),根据两点间的距离公式和勾股定理得(x+3)2+(![]() )2+(x﹣3)2+(
)2+(x﹣3)2+(![]() )2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个。
)2=36,此时P点有4个,③当∠PBA=90°时,P点的横坐标为3,此时P点有1个。


科目:初中数学 来源: 题型:
【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
(1)这50名同学捐款的众数为 元,中位数为 元。
(2)求这50名同学捐款的平均数。
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,将抛物线y=x2的对称轴绕着点P(0,2)顺时针旋转45°后与该抛物线交于A、B两点,点Q是该抛物线上一点.
(1)求直线AB的函数表达式。
(2)如图①,若点Q在直线AB的下方,求点Q到直线AB的距离的最大值
(3)如图②,若点Q在y轴左侧,且点T(0,t)(t<2)是射线PO上一点,当以P、B、Q为顶点的三角形与△PAT相似时,求所有满足条件的t的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为促销,决定对A,B两种商品进行打折出售.打折前,买6件A商品和3件B商品需要54元,买3件A商品和4件B商品需要32元;打折后,买50件A商品和40件B商品仅需364元,这比打折前少花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形
(2)判断直线EG是否经过一个定点,并说明理由
(3)求四边形EFGH面积的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,…,如此作下去,则△B2015A2016B2016的顶点A2016的坐标是 . 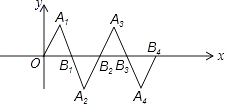
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com