
分析 (1)设x2=a,则原方程可化为a2-10a+9=0,求得a的值之后,继而可得x2=1或x2=9,解之即可;
(2)设$\frac{x+1}{{x}^{2}}$=m,则原方程可化为m-$\frac{2}{m}$=1,即m2-m-2=0,求得m的值后,即可得$\frac{x+1}{{x}^{2}}$=-1、$\frac{x+1}{{x}^{2}}$=2,解之即可;
(3)设x+$\frac{1}{x}$=y,则原方程可化为:y2-2-3y=2,即y2-3y-4=0,解之求得y之后,即可得x2+x+1=0或x2-4x+1=0,分别求解即可.
解答 解:(1)设x2=a,则原方程可化为a2-10a+9=0,
即(a-1)(a-9)=0,
解得:a=1或a=9,
当a=1时,x2=1,∴x=±1;
当a=9时,x2=9,∴x=±3;
(2)设$\frac{x+1}{{x}^{2}}$=m,则原方程可化为m-$\frac{2}{m}$=1,即m2-m-2=0,
∴(m+1)(m-2)=0,
解得:m=-1或m=2,
当m=-1时,$\frac{x+1}{{x}^{2}}$=-1,即x2+x+1=0,由△=1-4×1×1=-3<0知此时方程无解;
当m=2时,$\frac{x+1}{{x}^{2}}$=2,即2x2-x-1=0,解得:x=1或x=-$\frac{1}{2}$,
经检验x=1和x=-$\frac{1}{2}$都是原分式方程的解;
(3)设x+$\frac{1}{x}$=y,则原方程可化为:y2-2-3y=2,即y2-3y-4=0,
∴(y+1)(y-4)=0,
解得:y=-1或y=4,
当x+$\frac{1}{x}$=-1,即x2+x+1=0,由△=1-4×1×1=-3<0知此时方程无解;
当x+$\frac{1}{x}$=4,即x2-4x+1=0,解得:x=2$±\sqrt{3}$,
经检验x=2±$\sqrt{3}$是原分式方程的解.
点评 本题主要考查换元法解方程,把某个式子看作一个整体,用一个字母去代替它,实行等量替换是解题的关键.


科目:初中数学 来源: 题型:解答题
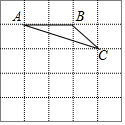 在如图所示的方格中,每个小正方形的边长为1,点A、B、C在方格纸中小正方形的顶点上.
在如图所示的方格中,每个小正方形的边长为1,点A、B、C在方格纸中小正方形的顶点上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
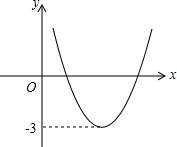 如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )
如图,已知函数y=ax2+bx+c的图象如图所示,那么关于x的方程ax2+bx+c+2=0的根的情况是( )| A. | 有两个同号不相等的实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 掷一枚均匀的正方形骰子,朝上一面的点数是5 | |
| B. | 任意选择某个电视频道,正在播放动画片 | |
| C. | 明天太阳从西边升起 | |
| D. | 抛出一枚硬币,落地后正面朝上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com