
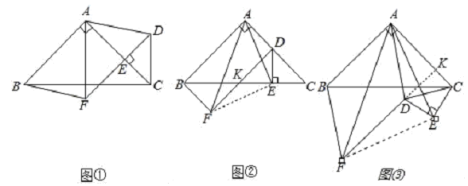
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

【答案】(1)AF=![]() AE;(2)AF=
AE;(2)AF=![]() AE,证明见解析;(3)结论不变,AF=
AE,证明见解析;(3)结论不变,AF=![]() AE,理由见解析.
AE,理由见解析.
【解析】
试题分析:(1)如图①中,结论:AF=![]() AE,只要证明△AEF是等腰直角三角形即可.(2)如图②中,结论:AF=
AE,只要证明△AEF是等腰直角三角形即可.(2)如图②中,结论:AF=![]() AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可.(3)如图③中,结论不变,AF=
AE,连接EF,DF交BC于K,先证明△EKF≌△EDA再证明△AEF是等腰直角三角形即可.(3)如图③中,结论不变,AF=![]() AE,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.
AE,连接EF,延长FD交AC于K,先证明△EDF≌△ECA,再证明△AEF是等腰直角三角形即可.
试题解析:(1)如图①中,结论:AF=![]() AE.
AE.
理由:∵四边形ABFD是平行四边形,
∴AB=DF,
∵AB=AC,
∴AC=DF,
∵DE=EC,
∴AE=EF,
∵∠DEC=∠AEF=90°,
∴△AEF是等腰直角三角形,
∴AF=![]() AE.
AE.
(2)如图②中,结论:AF=![]() AE.
AE.
理由:连接EF,DF交BC于K.
∵四边形ABFD是平行四边形,
∴AB∥DF,
∴∠DKE=∠ABC=45°,
∴EKF=180°﹣∠DKE=135°,
∵∠ADE=180°﹣∠EDC=180°﹣45°=135°,
∴∠EKF=∠ADE,
∵∠DKC=∠C,
∴DK=DC,
∵DF=AB=AC,
∴KF=AD,
在△EKF和△EDA中,
 ,
,
∴△EKF≌△EDA,
∴EF=EA,∠KEF=∠AED,
∴∠FEA=∠BED=90°,
∴△AEF是等腰直角三角形,
∴AF=![]() AE.
AE.
(3)如图③中,结论不变,AF=![]() AE.
AE.
理由:连接EF,延长FD交AC于K.
∵∠EDF=180°﹣∠KDC﹣∠EDC=135°﹣∠KDC,
∠ACE=(90°﹣∠KDC)+∠DCE=135°﹣∠KDC,
∴∠EDF=∠ACE,
∵DF=AB,AB=AC,
∴DF=AC
在△EDF和△ECA中,
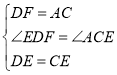 ,
,
∴△EDF≌△ECA,
∴EF=EA,∠FED=∠AEC,
∴∠FEA=∠DEC=90°,
∴△AEF是等腰直角三角形,
∴AF=![]() AE.
AE.


科目:初中数学 来源: 题型:
【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
(1)表中第6行的最后一个数是 ,第n行的最后一个数是 ;
(2)若用(a,b)表示一个数在数表中的位置,如9的位置是(4,3),则168的位置是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程承包方指定由甲、乙两个工程队完成某项工程,若由甲工程队单独做需要40天完成,现在甲、乙两个工程队共同做20天后,由于甲工程队另有其它任务不再做该工程,剩下工程由乙工程队再单独做了20天才完成任务.
(1)求乙工程队单独完成该工程需要多少天?
(2)如果工程承包方要求乙工程队的工作时间不能超过30天,要完成该工程,甲工程队至少要工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
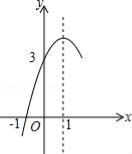
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明将父亲经营的便利店中“收入100元”记作“+100元”,那么“﹣80元”表示( )
A. 支出20元 B. 支出80元 C. 收入20元 D. 收入80元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校部分学生选择社团的意向,并将调查结果绘制成如下统计图(不完整):

根据统计图的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…,xn的n个正方形依次放入 △ABC中,请回答下列问题:
(1)按要求填表:
n | 1 | 2 | 3 |
xn |
(2)第n个正方形的边长xn= ;
(3)若m,n,p,q是正整数,且xmxn=xpxq,试判断m,n,p,q的关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com