
【题目】某工程承包方指定由甲、乙两个工程队完成某项工程,若由甲工程队单独做需要40天完成,现在甲、乙两个工程队共同做20天后,由于甲工程队另有其它任务不再做该工程,剩下工程由乙工程队再单独做了20天才完成任务.
(1)求乙工程队单独完成该工程需要多少天?
(2)如果工程承包方要求乙工程队的工作时间不能超过30天,要完成该工程,甲工程队至少要工作多少天?
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子中装有4个白球和3个黑球,它们除了颜色外都相同,随机从中摸出2个球,属于不可能事件的是( )
A.摸到2个白球
B.摸到2个黑球
C.摸到1个白球,1个黑球
D.摸到1个黑球,1个红球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1)试判断BE与FH的数量关系,并说明理由;
(2)求证:∠ACF=90°;
(3)如图2,过A、E、F三点作圆,若EC=4,∠CEF=15°,求AE的长.
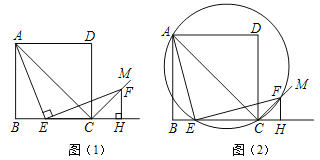
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,D为 BC的中点.
(1)如图(1),若点M、N分别是线段AB、AC的中点。求证:DM=DN
(2)如图(2),若点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△DMN的形状,并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2图象向左平移1个单位,再向下平移2个单位后,所得图象的函数是( )
A.y=(x+1)2+2
B.y=(x﹣1)2﹣2
C.y=(x+1)2﹣2
D.y=(x﹣1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会会期为2010年5月1日至2010年10月31日。门票设个人票和团队票两大类。个人普通票160元/张,学生优惠票100元/张;成人团队票120元/张,学生团队票50元/张。
(1)如果2名老师、10名学生均购买个人票去参观世博会,请问一共要花多少元钱购买门票?
(2)用方程组解决下列问题:如果某校共30名师生去参观世博会,并得知他们都是以团队形式购买门票,累计花去2200元,请问该校本次分别有多少名老师、多少名学生参观世博会?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在五张正面分别写有数字﹣2,﹣1,0,1,2的卡片,它们的背面完全相同,现将这五张卡片背面朝上洗匀.
(1)从中任意抽取一张卡片,则所抽卡片上数字的绝对值不大于1的概率是 ;
(2)先从中任意抽取一张卡片,以其正面数字作为a的值,然后再从剩余的卡片随机抽一张,以其正面的数字作为b的值,请用列表法或画树状图法,求点Q(a,b)在第二象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠BAC=90°,AB=AC,点E在AC上(且不与点A,C重合),在△ABC的外部作△CED,使∠CED=90°,DE=CE,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)请直接写出线段AF,AE的数量关系 ;
(2)将△CED绕点C逆时针旋转,当点E在线段BC上时,如图②,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
(3)在图②的基础上,将△CED绕点C继续逆时针旋转,请判断(2)问中的结论是否发生变化?若不变,结合图③写出证明过程;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某冷库一天的冷冻食品进出记录如表(运进用正数表示,运出用负数表示):

(1)这天冷库的冷冻食品比原来增加了还是减少了?请说明理由;
(2)根据实际情况,现有两种方案:
方案一:运进每吨冷冻食品费用500元,运出每吨冷冻食品费用800元;
方案二:不管运进还是运出每吨冷冻食品费用都是600元;
从节约运费的角度考虑,选用哪一种方案比较合适.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com