
����Ŀ��ˮ���е�ţ���ͽ��ӵ�ά���غ����ܸߣ������������ϲ������ũ�����ˮ���̼�11�·ݹ����˵�һ��ţ���ͽ��ӹ�300ǧ�ˣ���֪ţ������ÿǧ��15Ԫ���ۼ�ÿǧ��30Ԫ�����ӽ���ÿǧ��5Ԫ���ۼ�ÿǧ��10Ԫ��
(1)������ţ���ͽ���ȫ�����������������3500Ԫ����ţ�����ٹ�������ǧ�ˣ�
(2)��һ��ţ���ͽ��Ӻܿ����꣬�����̼Ҿ��������ڶ���ţ���ͽ��ӣ�ţ���ͽ��ӵĽ��۲��䣬ţ���ۼ۱ȵ�һ������a%(����aΪ������)�������ۼ۱ȵ�һ������2a%��������(1)�л���������ʱ��������ȣ�ţ���������½�a%�����ӵ��������ֲ��䣬����ڶ������Ѿ�������ţ���ͽ��ӵ������ܶ��(1)�е�һ��ţ���ͽ�����������Ӧ��������ܶ�������2%����������a��ֵ��
���𰸡���1��ţ�����ٹ���200ǧ�ˣ���2��������a��ֵΪ10
��������
��1���蹺��ţ��xǧ�ˣ������ӣ�300-x��ǧ�ˣ�����������=ÿǧ������������������ϻ���������3500Ԫ�����ɵó�����x��һԪһ�β���ʽ����֮ȡ����Сֵ���ɵó����ۣ�
��2�����������ܶ�=���۵������������������ɵó�����a��һԪ���η��̣���֮ȡ����ֵ���ɵó����ۣ�
��1���蹺��ţ��xǧ�ˣ������ӣ�300��x��ǧ�ˣ�
����������30��15��x+��10��5����300��x����3500��
��ã�x��200��
��ţ�����ٹ���200ǧ�ˣ�
��2����������ã�30��1+a%����200��1��a%��+10��1+2a%����100
=[30��200+10��100] ����1+2%��
�����ã�-![]() a2+20a=140��
a2+20a=140��
��ã�a1=10��a2=![]() ���������⣬��ȥ����
���������⣬��ȥ����
��������a��ֵΪ10��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
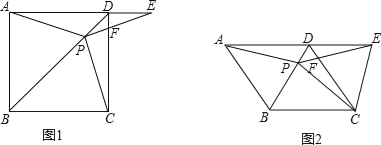
����Ŀ����ͼ1����������ABCD�У�P�ǶԽ���BD�ϵ�һ�㣬��E��AD���ӳ����ϣ���PA=PE��PE��CD��F��
��1��֤����PC=PE��
��2������CPE�Ķ�����
��3����ͼ2����������ABCD��Ϊ����ABCD�������������䣬����ABC=120��ʱ������CE����̽���߶�AP���߶�CE��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
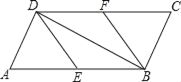
����Ŀ����ͼ��ƽ���ı���ABCD�У�E��F�ֱ�Ϊ��AB��CD���е㣬BD�ǶԽ��ߣ�����ADB��ֱ�ǣ���֤���ı���BFDE�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
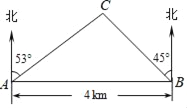
����Ŀ����ͼ����һ��ֱ�ĺ���������A��B�����۲�㣬B��A����������AB��4km����A��õ���C�ڱ�ƫ��53�������ϣ���B��õ���C�ڱ�ƫ��45�������ϣ������C��۲��A�ľ���(��ȷ��0.1km)��(�ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��sin53���0.80��cos53���0.60��tan53���1.33)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
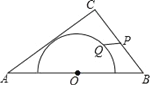
����Ŀ����ͼ���ڡ�ABC�У�AB=10��AC=8��BC=6���Ա�AB���е�OΪԲ�ģ�����Բ��AC���У���P��Q�ֱ��DZ�BC�Ͱ�Բ�ϵĶ��㣬����PQ����PQ������Сֵ��_______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
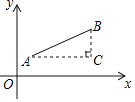
����Ŀ������ֽ��ÿ��С�����εı߳����ǵ�λ1����OAB��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ��������⣺
��1���밴Ҫ�����ABO�����±任��
������OAB����ƽ��2����λ��������ƽ��3����λ�õ���O1A1B1��
���Ե�OΪλ�����ģ�λ�Ʊ�Ϊ2��1������ABC��λ�����ĵ������зŴ�õ���OA2B2��
��2��д����A1��A2�����꣺ �� ��
��3����OA2B2�����Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����������ϣ��ش����⣺
����һ�����ǽ�![]() ��
��![]() ��Ϊһ�ԡ���żʽ����Ϊ
��Ϊһ�ԡ���żʽ����Ϊ![]() �����Թ��조����ʽ����˿�����Ч�ؽ�
�����Թ��조����ʽ����˿�����Ч�ؽ�![]() ��
��![]() �е�
�е�![]() ȥ��.���磺��֪
ȥ��.���磺��֪![]() ����
����![]()
![]() ��ֵ���⣺
��ֵ���⣺![]() ��
��![]()
���϶�����ͼ����![]() ����
����![]() ����ABΪб����
����ABΪб����![]() ����
����![]() ������
������![]() ��
��![]() ������
������![]() .��֮���ɽ�����ʽ
.��֮���ɽ�����ʽ![]() ��ֵ������
��ֵ������![]() ����
����![]() �ľ���.
�ľ���.
���磺![]() =
=![]() ��
��
���Կɽ�����ʽ![]() ��ֵ������
��ֵ������![]() ����
����![]() �ľ��룮
�ľ��룮
![]() ���ò���һ�������x�ķ��̣�
���ò���һ�������x�ķ��̣�![]() ������
������![]() ��
��
![]() ���ò��϶��������ʽ
���ò��϶��������ʽ![]() ����Сֵ���������ʱy��x�ĺ�����ϵʽ��д��x��ȡֵ��ͼ��
����Сֵ���������ʱy��x�ĺ�����ϵʽ��д��x��ȡֵ��ͼ��
![]() ��
��![]() ���õ�y��x�ĺ�����ϵʽ��x��ȡֵ��Χ����
���õ�y��x�ĺ�����ϵʽ��x��ȡֵ��Χ����![]() �н��x��ֱ��д��x��ֵ��
�н��x��ֱ��д��x��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������·�������ƾ��÷�չ�����������ҹ�����ʮ��������·���裮������·ͨ�������쵽�Ϻ���ԭ��·ȫ��������320ǧ�ף��г��������ʱ�ٱ�ԭ��·�������ʱ�������120ǧ��/Сʱ��ȫ���������ʱ��ֻ��8Сʱ����ԭ��·�������ʱ������16Сʱ��
��1��������·ͨ�������쵽�Ϻ����г������������Ƕ���ǧ�ף�
��2��ר�ҽ��飺�Ӱ�ȫ�ĽǶȿ��ǣ�ʵ������ʱ�ټ���m%���Ա����г��ʱ��Ӧ��ͻ���¼��������������쵽�Ϻ���ʵ������ʱ�佫����![]() m%Сʱ����m��ֵ��
m%Сʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͼ�ν�����������Ӧ��ʮ�ֹ㷺���ر�����Щ�����Ժ�ǿ����Ŀ��������ܷ�����Ŀ���������ļ������壬����ͨ���Ĵ�������ȥ˼�������������������룬�������֣���ʱ�������ת��˼ά��������Ŀ�������ļ���������ͨ�������ʺϵļ���ͼ�Σ�����õ��°빦����Ч���������������ʵ����
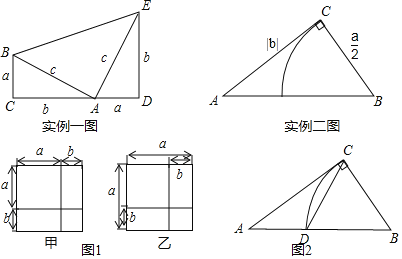
ʵ��һ��1876�꣬������ͳ٤�Ƕ�������ʵ��һͼ֤���˹��ɶ�������S�ı���ABCD=S��ABC+S��ADE+S��ABE�ã�![]() ��a+b��2=2��
��a+b��2=2��![]() ab+
ab+![]() c2������ã�a2+b2=c2��
c2������ã�a2+b2=c2��
ʵ������ŷ����õġ�����ԭ�������أ�����x�ķ���x2+ax=b2��ͼ�ⷨ�ǣ���Rt��ABC��ʹ��ACB=90����BC=![]() ��AC=|b|������б��AB�Ͻ�ȡBD=
��AC=|b|������б��AB�Ͻ�ȡBD=![]() ����AD�ij����Ǹ÷��̵�һ����������ʵ����ͼ����
����AD�ij����Ǹ÷��̵�һ����������ʵ����ͼ����
����������Ķ����ϻش���������⣺
��1����ͼ1��������ͼ��������ĵ�����ϵ��д����ͼҪ֤������ѧ��ʽ��______����ͼҪ֤������ѧ��ʽ��______�����ֵ���ѧ˼����______��
��2����ͼ2����2��-8�ǹ���x�ķ���x2+ax=b2��������������ʵ�����ķ�ʽ����Rt��ABC������CD����CD�ij���
��3����x��y��z��Ϊ��������x2+y2=z2�����ù���ͼ�εķ�����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com