
【题目】如图,平行四边形![]() 的对角线
的对角线![]() ,
,![]() 相交于点
相交于点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() .
.
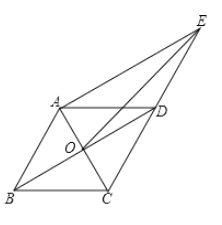
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)连接![]() ,若
,若![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明间解析;(2)![]()
【解析】
(1)四边形ABCD是平行四边形,由平行四边形的性质,及![]() ,可得AB=DE, AB//DE ,则四边形ABDE是平行四边形;
,可得AB=DE, AB//DE ,则四边形ABDE是平行四边形;
(2)因为AD=DE=8,则AD=AB=8,四边形ABCD是菱形,由菱形的性质及解直角三角形可得AO=ABsin∠ABO=4,BO=ABcos∠ABO=4![]() , BD=8
, BD=8![]() ,则AE=BD,利用勾股定理可得OE.
,则AE=BD,利用勾股定理可得OE.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DE=CD,
∴AB=DE.
又∵AB∥DE
∴四边形ABDE是平行四边形;
(2)∵AD=DE=8,
∴AD=AB=8.
∴ABCD是菱形,
∴AB=BC,AC⊥BD,![]() ,
,![]() .
.
又∵∠ABC=60°,
∴∠ABO=30°.
在Rt△ABO中,![]() ,
,![]() .
.
∴![]() .
.
∵四边形ABDE是平行四边形,
∴AE∥BD,![]() .
.
又∵AC⊥BD,
∴AC⊥AE.
在Rt△AOE中,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
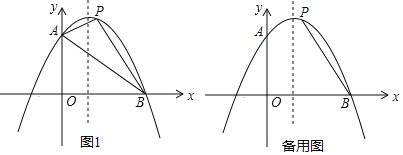
【题目】如图1,已知抛物线y=ax2+2x+c(a≠0),与y轴交于点A(0,6),与x轴交于点B(6,0).
(1)求这条抛物线的表达式及其顶点坐标;
(2)设点P是抛物线上的动点,若在此抛物线上有且只有三个P点使得△PAB的面积是定值S,求这三个点的坐标及定值S.
(3)若点F是抛物线对称轴上的一点,点P是(2)中位于直线AB上方的点,在抛物线上是否存在一点Q,使得P、Q、B、F为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】奇异果是新西兰的特产,其实它的祖籍在中国,又名“猕猴桃”.2018年1月份至6月份我市某大型超市新西兰品种的奇异果销售价格y(元/盒)与月份x(1≤x≤6,且x为整数)之间的函数关系如下表:

7月份至12月份奇异果的销售价格y(元/盒)与月份x之间满足函数关系式:y=2x+20(7≤x≤12且x为整数).该超市去年奇异果销售数量z(盒)与月份x(1≤x≤12,且x为整数)之间存在如图所示的变化趋势.若去年该超市奇异果的进价为每盒20元,销售奇异果需要一名超市员工,该员工每月固定人工费用为1500元.
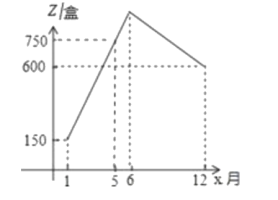
(1)请观察图表中的数据信息直接写出2018年1月份至6月份销售价格y与x之间的函数关系式__ ,根据如图所示的变化趋势,直接写出去年每月销售数量z与x之间满足的函数关系式__ .
(2)求出去年每月该超市的利润w(元)与月份x之间满足的函数关系式.(利润=收入成本费用)
(3)从今年1月份开始,超市决定每卖出一盒奇异果,公司向希望工程捐款2元,奇异果的进价为每盒26元,虽然今年1月份奇异果的销售价格比去年12月份增加4元,但1月份销售数量仍比去年12月份增加了0.4a%;2月份销售价格在1月份的基础上增加了0.5a%,由于其它水果陆续上市,2月份的销售量与1月份持平,这样2月份的利润达到了15780元,请参考以下数据,求出整数a的值.(参考数据:![]() =2025,
=2025,![]() =2116,
=2116,![]() =2209)
=2209)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的道路AB上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,假设他们分别以不同的速度匀速行驶,甲先出发6分钟后,乙才出发,乙的速度为![]() 千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
千米/分,在整个过程中,甲、乙两人之间的距离y(千米)与甲出发的时间x(分)之间的部分函数图象如图.
(1)A、B两地相距____千米,甲的速度为____千米/分;
(2)求线段EF所表示的y与x之间的函数表达式;
(3)当乙到达终点A时,甲还需多少分钟到达终点B?

查看答案和解析>>
科目:初中数学 来源: 题型:
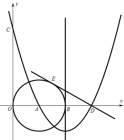
【题目】如图,已知点![]() ,以
,以![]() 为圆心作
为圆心作![]() 与
与![]() 轴切于原点,与
轴切于原点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,过
,过![]() 作
作![]() 的切线
的切线![]() .
.
(1)以直线![]() 为对称轴的抛物线过点
为对称轴的抛物线过点![]() 及点
及点![]() ,求次抛物线的解析式;
,求次抛物线的解析式;
(2)第(1)问中的抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() ,过
,过![]() 作
作![]() 的切线
的切线![]() ,
,![]() 为切点,求此切线长;
为切点,求此切线长;
(3)点![]() 是切线DE上的一个动点,当
是切线DE上的一个动点,当![]() 与
与![]() 相似时,求出点
相似时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接![]() 年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为
年中、日、韩三国青少年橄榄球比赛,南雅中学计划对面积为![]() 运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的
运动场进行塑胶改造.经投标,由甲、乙两个工程队来完成,已知甲队每天能改造的面积是乙队每天能改造面积的![]() 倍,并且在独立完成面积为
倍,并且在独立完成面积为![]() 的改造时,甲队比乙队少用
的改造时,甲队比乙队少用![]() 天.
天.
(1)求甲、乙两工程队每天能完成塑胶改造的面积;
(2)设甲工程队施工![]() 天,乙工程队施工
天,乙工程队施工![]() 天,刚好完成改造任务,求
天,刚好完成改造任务,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(3)若甲队每天改造费用是![]() 万元,乙队每天改造费用是
万元,乙队每天改造费用是![]() 万元,且甲、乙两队施工的总天数不超过
万元,且甲、乙两队施工的总天数不超过![]() 天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
天,如何安排甲、乙两队施工的天数,使施工总费用最低?并求出最低的费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,M是BC的中点,且AM=9,BD=12,AD=10,则ABCD的面积是( )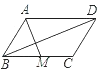
A. 30B. 36C. 54D. 72
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com