【题目】在下列说法中 ①0.09是0.81的平方根；②－9的平方根是±3；③
的算术平方根是－5；④
是一个负数；⑤0的相反数和倒数都是0；⑥
；⑦如果一个数的立方根是这个数的本身，那么这个数是1或0；⑧全体实数和数轴上的点一一对应．正确的有_________．
发散思维新课堂系列答案科目：初中数学 来源： 题型：
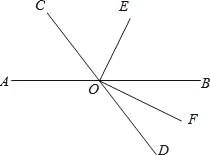
【题目】如图，直线AB与CD相交于O．OF是∠BOD的平分线，OE⊥OF．
（1）若∠BOE比∠DOF大38°，求∠DOF和∠AOC的度数；
（2）试问∠COE与∠BOE之间有怎样的大小关系？请说明理由．
（3）∠BOE的余角是 ，∠BOE的补角是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，任意一个正整数n都可以进行这样的分解：
（p，q是正整数，且
），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的完美分解．并规定：
．
例如18可以分解成1×18，2×9或3×6，因为18－1＞9－2＞6－3，所以3×6是18的完美分解，所以F（18）＝
．
（1）F（13）＝ ，F（24）＝ ；
（2）如果一个两位正整数t，其个位数字是a，十位数字为
，交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数为“和谐数”，求所有“和谐数”；
（3）在（2）所得“和谐数”中，求F（t）的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
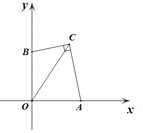
【题目】如图，在平面直角坐标系xOy中，A,B两点分别在x轴，y轴的正半轴上，且OA=OB，点C在第一象限，OC=3，连接BC，AC，若∠BCA=90°，则BC+AC的值为_________。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：在分式中，对于只含有一个字母的分式，当分子的次数小于分母的次数时，我们称之为“真分式”，如：
。当分子的次数大于或等于分母的次数时，我们称之为“假分式”，如：
。假分式可以化为整式与真分式和的形式，我们也称之为带分式，如：
。
解决问题：
（1）下列分式中属于真分式的是（ ）
A.
B.
C.
D.
（2）将假分式
分别化为带分式；
（3）若假分式
的值为整数，请直接写出所有符合条件的整数x的值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的方程x2＋(2k－1)x＋k2－1＝0有两个实数根x1，x2．
(1)求实数k的取值范围；
(2)若x1，x2满足x12＋x22＝16＋x1x2，求实数k的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
为
的中点，
，
.动点
从点
出发，沿
方向以
的速度向点
运动；同时动点
从点出发，沿
方向以的速度向点
运动，运动时间是
秒.
（1）用含的代数式表示
的长度.
（2）在运动过程中，是否存在某一时刻，使点位于线段
的垂直平分线上？若存在，求出的值；若不存在，请说明理由.
（3）是否存在某一时刻，使
？若存在，求出的值；若不存在，请说明理由.
（4）是否存在某一时刻，使
？若存在，求出的值；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某超市预测某饮料会畅销、先用1800元购进一批这种饮料，面市后果然供不应求，又用8100元购进这种饮料，第二批饮料的数量是第一批的3倍，但单价比第一批贵2元．
（1）第一批饮料进货单价多少元？
（2）若两次进饮料都按同一价格销售，两批全部售完后，获利不少于2700元，那么销售单价至少为多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
