
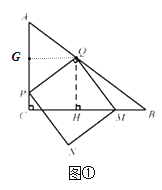
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚ![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ”ă
ŁŹ”ă![]() ŽÓ”ă
ŽÓ”ă![]() łö·ąŁŹŃŰŐÛÏß
łö·ąŁŹŃŰŐÛÏß![]() ÒÔĂżĂë
ÒÔĂżĂë![]() žö”„λł€¶È”ÄËÙ¶ÈÏòÖŐ”ă
žö”„λł€¶È”ÄËÙ¶ÈÏòÖŐ”ă![]() Ô˶ŻĄŁ”±”ă
Ô˶ŻĄŁ”±”ă![]() Č»Óë”ă
Č»Óë”ă![]() Ąą
Ąą![]() ÖŰșÏʱŁŹÔÚ±ß
ÖŰșÏʱŁŹÔÚ±ß![]() ÉÏÈĄÒ»”ă
ÉÏÈĄÒ»”ă![]() ŁŹÂúŚă
ŁŹÂúŚă![]() ŁŹčę”ă
ŁŹčę”ă![]() Śś
Śś![]() ŁŹœ»±ß
ŁŹœ»±ß![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹÒÔ
ŁŹÒÔ![]() Ąą
Ąą![]() ÎȘ±ßŚöŸŰĐÎ
ÎȘ±ßŚöŸŰĐÎ![]() .Éè”ă
.Éè”ă![]() ”ÄÔ˶ŻÊ±ŒäÎȘ
”ÄÔ˶ŻÊ±ŒäÎȘ![]() Ăë.
Ăë.
Łš1Ł©ÓĂșŹ![]() ”ÄŽúÊęÊœ±íÊŸÏ߶Î
”ÄŽúÊęÊœ±íÊŸÏ߶Î![]() ”Äł€;
”Äł€;
Łš2Ł©”±ŸŰĐÎ![]() ÎȘŐę·œĐÎʱŁŹÇó
ÎȘŐę·œĐÎʱŁŹÇó![]() ”ÄÖ”;
”ÄÖ”;
Łš3Ł©ÉèŸŰĐÎ![]() Óë
Óë![]() ÖŰ”țČż·ÖÍŒĐΔÄÖÜł€ÎȘ
ÖŰ”țČż·ÖÍŒĐΔÄÖÜł€ÎȘ![]() ŁŹÇó
ŁŹÇó![]() Óë
Óë![]() ÖźŒä”ÄșŻÊęčŰϔʜ;
ÖźŒä”ÄșŻÊęčŰϔʜ;
Łš4Ł©Śś”ă![]() čŰÓÚÖ±Ïß
čŰÓÚÖ±Ïß![]() ”Ä¶ÔłÆ”ă
”Ä¶ÔłÆ”ă![]() ŁŹŚś”ă
ŁŹŚś”ă![]() čŰÓÚÖ±Ïß
čŰÓÚÖ±Ïß![]() ”Ä¶ÔłÆ”ă
”Ä¶ÔłÆ”ă![]() .”±
.”±![]() Ąą
Ąą![]() ŐâÁœ”ăÖĐÖ»ÓĐÒ»žö”ăÔÚŸŰĐÎ
ŐâÁœ”ăÖĐÖ»ÓĐÒ»žö”ăÔÚŸŰĐÎ![]() ÄÚČżÊ±ŁŹÖ±œÓĐŽłöŽËʱ
ÄÚČżÊ±ŁŹÖ±œÓĐŽłöŽËʱ![]() ”ÄÈĄÖ”·¶Î§.
”ÄÈĄÖ”·¶Î§.
ĄŸŽđ°žĄżŁš1Ł©”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ”±
ŁŹ”±![]() ʱŁŹ
ʱŁŹ![]() Ł»Łš2Ł©”±ŸŰĐÎ
Ł»Łš2Ł©”±ŸŰĐÎ![]() ÎȘŐę·œĐÎʱŁŹ
ÎȘŐę·œĐÎʱŁŹ![]() ”ÄÖ”ÎȘ
”ÄÖ”ÎȘ![]() Ł»Łš3Ł©”±
Ł»Łš3Ł©”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ”±
ŁŹ”±![]() ʱŁŹ
ʱŁŹ ![]() Ł»Łš4Ł©
Ł»Łš4Ł©![]() »ò
»ò![]() .
.
ĄŸœâÎöĄż
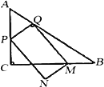
Łš1Ł©”±”ăPÔÚACÉÏʱŁŹŃÓł€ACÖÁ”ăDŁŹÊč”ĂCD=ACŁŹÒŚ”ĂĄÏABD=2ĄÏABC=ĄÏPQAŁŹżÉ”ĂPQĄÎDBŁŹ”ĂĄśAPQĄŚĄśADBŁŹžùŸĘÏàËÆÈęœÇĐΔĶÔÓŠ±ßłÉ±ÈÀęÁĐłö”ÈÊœ±äĐÎŒŽżÉ”ĂłöœáÂÛŁ»
”±”ăPÔÚCBÉÏʱŁŹčę”ăQŚśQEĄÍBCŁŹÓÉĄÏPQA=2ĄÏBșÍÈęœÇĐÎÍâœÇ”ÄĐÔÖÊżÉ”ĂĄśQPBÎȘ”ÈŃüÈęœÇĐÎŁŹžùŸĘĄ°ÈęÏßșÏÒ»Ą±żÉ”ĂBE=![]() BP=
BP=![]() (7-t)ŁŹÈ»șóÓÉĄśBQEĄŚĄśBACÁĐłö±ÈÀęÊœŒŽżÉ”ĂłöœáÂÛŁ»
(7-t)ŁŹÈ»șóÓÉĄśBQEĄŚĄśBACÁĐłö±ÈÀęÊœŒŽżÉ”ĂłöœáÂÛŁ»
Łš2Ł©”±”ăPÔÚACÉÏʱŁŹčęPŚśQGĄÍACŁŹQHĄÍBCŁŹÓÉŁš1Ł©żÉ”ĂĄśAQPÊÇ”ÈŃüÈęœÇĐÎŁŹżÉ”ĂGP=![]() tŁŹžùŸĘŸŰĐΔÄĆжš”ĂËıßĐÎGQHCÎȘŸŰĐÎŁŹ”ĂłöQH=GC=3-
tŁŹžùŸĘŸŰĐΔÄĆжš”ĂËıßĐÎGQHCÎȘŸŰĐÎŁŹ”ĂłöQH=GC=3-![]() tŁŹžùŸĘÔČÄÚœÓËıßĐΔĶԜǻ„ČčșÍ”ÈŃüÈęœÇĐΔÄĐÔÖÊ”ĂłöĄÏA=ĄÏQMHŁŹœű¶űżÉ”ĂĄśQHMĄŚĄśBCAŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊÁĐłö±ÈÀęÊœÇółöQMŁŹÁîQM=PQŒŽżÉÇółötŁ»”±PÔÚBCÉÏʱŁŹČ»ÄÜččłÉŐę·œĐÎŁŹŚÛÉÏŒŽżÉ”ĂłöœáÂÛŁ»
tŁŹžùŸĘÔČÄÚœÓËıßĐΔĶԜǻ„ČčșÍ”ÈŃüÈęœÇĐΔÄĐÔÖÊ”ĂłöĄÏA=ĄÏQMHŁŹœű¶űżÉ”ĂĄśQHMĄŚĄśBCAŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊÁĐłö±ÈÀęÊœÇółöQMŁŹÁîQM=PQŒŽżÉÇółötŁ»”±PÔÚBCÉÏʱŁŹČ»ÄÜččłÉŐę·œĐÎŁŹŚÛÉÏŒŽżÉ”ĂłöœáÂÛŁ»
Łš3Ł©”±”ăPÔÚACÉÏʱŁŹÒŚ”ĂĄÏCPK=ĄÏKMN=ĄÏBŁŹÀûÓĂÈęœÇșŻÊężÉÇó”ĂPKŁŹMK”ÄÖ”ŁŹÈ»șóŽúÈëŒÆËăPQ+QM+MK+PKŒŽżÉŁ»
”±”ăPÔÚBCÉÏʱŁŹÓÉŁš1Ł©żÉ”ĂĄÏQPM=ĄÏBŁŹÔÚRtĄśQPMÖĐŁŹÀûÓĂÈęœÇșŻÊężÉÇó”ĂQMŁŹPM”Äł€ŁŹÈ»șóŽúÈëŒÆËăŒŽżÉŁ»
Łš4Ł©”±”ăPÔÚACÉÏʱŁŹčę”ăAŚśADĄÍPQŁŹčę”ăCŚśCEĄÍPNŁŹ·Ö”ăAĄäÔÚŸŰĐÎPQMNÄÚČżĄą”ăCĄäČ»ÔÚŸŰĐÎPQMNÄÚČżșÍ”ăAĄäČ»ÔÚŸŰĐÎPQMNÄÚČżĄą”ăCĄäÔÚŸŰĐÎPQMNÄÚČżŁŹŒŽ![]() șÍ
șÍ![]() ÁœÖÖÇéżöÇółöt”Ä·¶Î§Ł»”±”ăPÔÚBCÉÏʱŁŹÏÔÈ»”ăAĄäșÍ”ăCĄä¶ŒÔÚŸŰĐÎPQMNÍâČżŁź
ÁœÖÖÇéżöÇółöt”Ä·¶Î§Ł»”±”ăPÔÚBCÉÏʱŁŹÏÔÈ»”ăAĄäșÍ”ăCĄä¶ŒÔÚŸŰĐÎPQMNÍâČżŁź
œâŁșŁš1Ł©”±”ăPÔÚACÉÏʱŁŹŒŽ0ŁŒtĄÜ3ʱŁŹŃÓł€ACÖÁ”ăDŁŹÊč”ĂCD=ACŁŹ
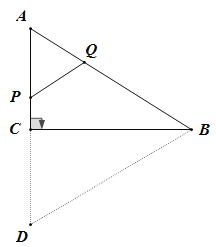
ÔÚRtĄśABCÖĐŁŹAC=3ŁŹBC=4ŁŹ
ĄàAB=5Łź
ÔÚĄśABCșÍĄśDBCÖĐŁŹ
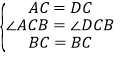 ŁŹ
ŁŹ
ĄàĄśABCĄŐĄśDBCŁšSASŁ©ŁŹ
ĄàAC=CD=3ŁŹAB=CD=5ŁŹĄÏABC=ĄÏDBCŁź
ĄßĄÏPQA=2ĄÏABCŁŹ
ĄàĄÏPQA=ĄÏABDŁŹ
ĄàPQĄÎBDŁŹ
ĄàĄśAPQĄŚĄśADBŁŹ
Ąà![]() ŁŹ
ŁŹ
ŒŽ![]() ŁŹ
ŁŹ
”ĂPQ=![]() Ł»
Ł»
”±”ăPÔÚCBÉÏʱŁŹŒŽ3ŁŒtŁŒ7ʱŁŹ
čę”ăQŚśQEĄÍBCÓÚ”ăEŁŹ
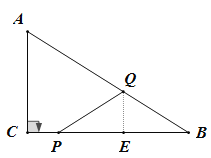
ĄßĄÏPQA=ĄÏB+ĄÏQPBŁŹĄÏPQA=2ĄÏBŁŹ
ĄàĄÏQPB=ĄÏBŁŹ
ĄàPQ=QBŁŹ
ĄàBE=![]() PB=
PB=![]() (7-t)ŁŹ
(7-t)ŁŹ
ĄßĄÏC=90ĄăŁŹ
ĄàQEĄÎACŁŹ
Ąà![]() ŁŹ
ŁŹ
ŒŽ![]() ŁŹ
ŁŹ
œâ”ĂŁșQB=![]() ŁŹ
ŁŹ
ĄàPQ=![]() Ł»
Ł»
ŚÛÉÏŁŹ”±![]() ʱŁŹ
ʱŁŹ![]() ŁŹ”±
ŁŹ”±![]() ʱŁŹ
ʱŁŹ![]() .
.
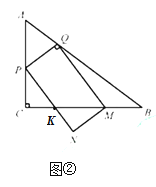
Łš2Ł©”±![]() ʱŁŹÈçÍŒąÙŁŹ
ʱŁŹÈçÍŒąÙŁŹ
čę”ă![]() ŚśQGĄÍACÓÚ”ăGŁŹ
ŚśQGĄÍACÓÚ”ăGŁŹ![]() ÓÚ”ă
ÓÚ”ă![]() .
.
ÓÉŁš1Ł©żÉ”ĂAQ=PQŁŹ
ĄàĄÏA=ĄÏAPQŁŹAG=GP=![]() AP=
AP=![]() tŁŹ
tŁŹ
ĄàCG=AC-AG=3-![]() tŁź
tŁź
ĄßĄÏQGC=ĄÏC=ĄÏQHC=90ĄăŁŹ
ĄàËıßĐÎQGCHÎȘŸŰĐÎŁŹ
ĄàQH=CG=3-![]() tŁź
tŁź
ĄßĄÏC=ĄÏPQM=90ĄăŁŹ
ĄàĄÏAPQ=ĄÏQMHŁŹ
ĄàĄÏA=ĄÏQMHŁŹ
ĄßĄÏQHM=ĄÏC=90ĄăŁŹ
ĄàĄśQHMĄŚĄśBCAŁŹ
Ąà![]() ŁŹ
ŁŹ
ŒŽ![]() ŁŹ
ŁŹ
Ąà![]() .
.
”±ŸŰĐÎ![]() ÎȘŐę·œĐÎʱŁŹ
ÎȘŐę·œĐÎʱŁŹ
![]() .
.
œâ”Ă![]() .
.
”±![]() ʱŁŹŸŰĐÎ
ʱŁŹŸŰĐÎ![]() Č»żÉÄÜÎȘŐę·œĐÎ.
Č»żÉÄÜÎȘŐę·œĐÎ.
Ąà”±ŸŰĐÎ![]() ÎȘŐę·œĐÎʱŁŹ
ÎȘŐę·œĐÎʱŁŹ![]() ”ÄÖ”ÎȘ
”ÄÖ”ÎȘ![]() .
.
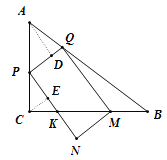
Łš3Ł©”±![]() ʱŁŹÈçÍŒąÚŁŹ
ʱŁŹÈçÍŒąÚŁŹ
ÓÉŁš1Ł©żÉ”ĂĄÏCPK=ĄÏKMN=ĄÏBŁŹ
ÔÚRtĄśPCKÖĐŁŹ
PK=![]() =
=![]() =
=![]() ŁŹ
ŁŹ
ÔÚRtĄśKNMÖĐŁŹ
MK=![]() =
=![]() ŁŹ
ŁŹ
![]() .
.
”±![]() ʱŁŹÈçÍŒąÛŁŹ
ʱŁŹÈçÍŒąÛŁŹ

ÓÉŁš1Ł©żÉ”ĂĄÏQPM=ĄÏBŁŹ
ÔÚRtĄśQPMÖĐŁŹ
QM=PQtanĄÏQPM=![]() ŁŹ
ŁŹ
PM=![]() =
=![]() =
=![]() ŁŹ
ŁŹ
![]() .
.
Łš4Ł©”±”ăPÔÚACÉÏʱŁŹ0ŁŒtŁŒ3ŁŹ
čę”ăAŚśADĄÍPQÓÚ”ăDŁŹčę”ăCŚśCEĄÍPNÓÚ”ăEŁŹÈçÍŒËùÊŸŁș
ÓÉŁš1Ł©”ĂĄÏAPQ=ĄÏPCE=ĄÏBACŁŹ
ÔÚRtĄśADPÖĐŁŹAD=APsinĄÏAPQ=![]() ŁŹ
ŁŹ
ÔÚRtĄśPCEÖĐŁŹCE=CPcosĄÏPCE=![]() Łź
Łź
”±”ăAĄäÔÚŸŰĐÎPQMNÄÚČżĄą”ăCĄäČ»ÔÚŸŰĐÎPQMNÄÚČżÊ±ŁŹ
![]() ŁŹ
ŁŹ
ŒŽ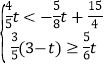 ŁŹ
ŁŹ
œâ”ĂŁștĄÜ![]() ŁŹ
ŁŹ
čÊ0ŁŒtĄÜ![]() Ł»
Ł»
”±”ăAĄäČ»ÔÚŸŰĐÎPQMNÄÚČżĄą”ăCĄäÔÚŸŰĐÎPQMNÄÚČżÊ±ŁŹ
![]() ŁŹ
ŁŹ
ŒŽ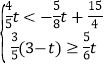 ŁŹ
ŁŹ
œâ”ĂŁștĄĘ![]() ŁŹ
ŁŹ
čÊ![]() ĄÜtŁŒ3Łź
ĄÜtŁŒ3Łź
”±”ăPÔÚBCÉÏʱŁŹÏÔÈ»”ăAĄäșÍ”ăCĄä¶ŒÔÚŸŰĐÎPQMNÍâČżŁź
čÊ![]() »ò
»ò![]() .
.


 ĐÄËăżÚËăÇÉËăÒ»żÎÒ»Á·Ï”ÁĐŽđ°ž
ĐÄËăżÚËăÇÉËăÒ»żÎÒ»Á·Ï”ÁĐŽđ°ž ÓŠÓĂÌâŚśÒ”±ŸÏ”ÁĐŽđ°ž
ÓŠÓĂÌâŚśÒ”±ŸÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘ·áž»ŽćĂńÒ”ÓàÎÄ»ŻÉú»îŁŹÄłżȘ·ąÇűÄłŽćĂńÎŻÔ±»á¶ŻÔ±ŽćĂńŚÔÔžŒŻŚÊœšÁąÒ»žöÊ饹±šĄążŻÔÄÀÀÊÒ.ŸÔ€ËăŁŹÒ»čČĐèÒȘłïŚÊ50000ÔȘŁŹÆäÖĐÒ»Čż·ÖÓĂÓÚčșÂòŚÀĄą”ÊĄąčń”ÈÉèÊ©ŁŹÁíÒ»Čż·ÖÓĂÓÚčșÂòÊ饹±šĄążŻ.
Łš1Ł©ŽćÎŻ»áŒÆ»źŁŹčșÂòÊ饹±šĄążŻ”ÄŚÊœđČ»ÉÙÓÚčșÂòŚÀĄą”ÊĄąčńŚÊœđ”Ä4±¶ŁŹÎÊŚî¶àÓöàÉÙŚÊœđčșÂòŚÀĄą”ÊĄąčń”ÈÉèÊ©Łż
Łš2Ł©ŸłőČœčÀŒÆŁŹÓĐ250»§ŽćĂńŚÔÔžČÎÓëŒŻŚÊŁŹÄÇĂŽÆœŸùĂż»§ĐèŒŻŚÊ200ÔȘ.żȘ·ąÇűčÜÎŻ»áÁËœâÇéżöșóŁŹÔùËÍÁËÒ»ĆúÔÄÀÀÊÒÉèÊ©șÍÊ饹±šĄążŻ.ŐâŃùŁŹÖ»ĐèČÎÓ뻧čČŒŻŚÊ36000ÔȘ.ŸŽćÎŻ»áœűÒ»ČœĐûŽ«ŁŹŚÔÔžČÎÓë”Ä»§ÊęÔÚ250»§”Ä»ùŽĄÉÏÔöŒÓÁË![]() ŁšÆäÖĐ
ŁšÆäÖĐ![]() Ł©.ÔòĂż»§ÆœŸùŒŻŚÊ”ÄŚÊœđÔÚ200ÔȘ”Ä»ùŽĄÉÏŒőÉÙÁË
Ł©.ÔòĂż»§ÆœŸùŒŻŚÊ”ÄŚÊœđÔÚ200ÔȘ”Ä»ùŽĄÉÏŒőÉÙÁË![]() ŁŹÇó
ŁŹÇó![]() ”ÄÖ”.
”ÄÖ”.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÁËŒÓǿѧÉú”Ä°ČÈ«ÒâʶŁŹÄłĐŁŚéÖŻÁËѧÉúČΌӰČÈ«ÖȘʶŸșÈüŁŹŽÓÖĐłéÈĄÁËČż·ÖѧÉúłÉŒšœűĐĐÍłŒÆŁŹČą°ŽŐŐłÉŒšŽÓ”Í”œžß·ÖłÉAŁŹBŁŹCŁŹDŁŹEÎćžöĐĄŚéŁŹ»æÖÆÍłŒÆÍŒÈçÏÂŁšÎŽÍêłÉŁ©ŁŹœâŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©Ńù±ŸÈĘÁżÎȘĄĄĄĄŁŹÆ”Êę·ÖČŒÖ±·œÍŒÖĐaŁœĄĄĄĄŁ»
Łš2Ł©ÉÈĐÎÍłŒÆÍŒÖĐDĐĄŚéËù¶ÔÓŠ”ÄÉÈĐÎÔČĐÄœÇÎȘnĄăŁŹÇón”Ä֔ȹČčÈ«Æ”Êę·ÖČŒÖ±·œÍŒŁ»
Łš3Ł©ÈôłÉŒšÔÚ80·ÖÒÔÉÏŁšČ»șŹ80·ÖŁ©ÎȘÓĆĐăŁŹÈ«ĐŁčČÓĐ2000ĂûѧÉúŁŹčÀŒÆłÉŒšÓĆĐă”ÄѧÉúÓжàÉÙĂûŁż

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
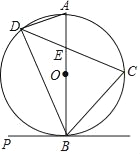
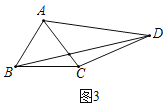
ĄŸÌâÄżĄżÈçÍŒŁŹCĄąDÊÇÒÔABÎȘÖ±Ÿ¶”ÄĄŃOÉÏ”Ä”ăŁŹ![]() ŁŹÏÒCDœ»ABÓÚ”ăEŁź
ŁŹÏÒCDœ»ABÓÚ”ăEŁź
Łš1Ł©”±PBÊÇĄŃO”ÄÇĐÏßʱŁŹÇóÖ€ŁșĄÏPBD=ĄÏDABŁ»
Łš2Ł©ÇóÖ€ŁșBC2©CE2=CEDEŁ»
Łš3Ł©ÒŃÖȘOA=4ŁŹEÊǰ럶OA”ÄÖД㣏ÇóÏ߶ÎDE”Äł€Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒ»žöȻ͞ܔĎüŚÓÖĐŚ°ÓĐșìĄą°ŚÁœÖÖŃŐÉ«”ÄĐĄÇòŁŹŐâĐ©ÇòłęŃŐÉ«ÍâÍêÈ«ÏàÍŹŁŹÆäÖĐșìÇòÓĐ![]() žöŁŹÈôŽÓÖĐËæ»úĂțłöÒ»žöÇòŁŹŐâžöÇòÊÇ°ŚÇò”ÄžĆÂÊÎȘ
žöŁŹÈôŽÓÖĐËæ»úĂțłöÒ»žöÇòŁŹŐâžöÇòÊÇ°ŚÇò”ÄžĆÂÊÎȘ![]() Łź
Łź
Łš![]() Ł©ÇëÖ±œÓĐŽłöŽüŚÓÖĐ°ŚÇò”ÄžöÊ꣟
Ł©ÇëÖ±œÓĐŽłöŽüŚÓÖĐ°ŚÇò”ÄžöÊ꣟
Łš![]() Ł©Ëæ»úĂțłöÒ»žöÇòșóŁŹ·Ć»ŰČąœÁÔÈŁŹÔÙËæ»úĂțłöÒ»žöÇòŁŹÇóÁœŽÎ¶ŒĂț”œÏàÍŹŃŐÉ«”ÄĐĄÇò”ÄžĆÂÊŁźŁšÇëœáșÏÊśŚŽÍŒ»òÁбíœâŽđŁ©
Ł©Ëæ»úĂțłöÒ»žöÇòșóŁŹ·Ć»ŰČąœÁÔÈŁŹÔÙËæ»úĂțłöÒ»žöÇòŁŹÇóÁœŽÎ¶ŒĂț”œÏàÍŹŃŐÉ«”ÄĐĄÇò”ÄžĆÂÊŁźŁšÇëœáșÏÊśŚŽÍŒ»òÁбíœâŽđŁ©
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
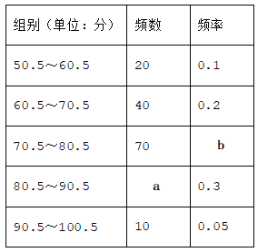
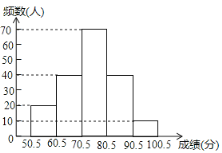
ĄŸÌâÄżĄżÎȘÔÚÖĐХѧÉúÖĐÆŐŒ°œ»Íš·ščæłŁÊ¶ŁŹł«”Œ°ČÈ«łöĐĐŁŹÄłÊĐœÌÓęŸÖÔÚÈ«ÊĐ·¶Î§ÄÚŚéÖŻÆßÄêŒ¶Ń§ÉúœűĐĐÁËÒ»ŽÎĄ°œ»čæŒÇĐÄŒäĄ±ÖȘʶŸșÈü.ÎȘÁËœâÊĐÆßÄêŒ¶Ń§Éú”ÄŸșÈüłÉŒšŁŹËæ»úłéÈĄÁËÈôžÉĂûѧÉú”ÄŸșÈüłÉŒšŁšłÉŒšÎȘŐûÊ꣏Âú·Ö100·ÖŁ©ŁŹœűĐĐÍłŒÆșóŁŹ»æÖÆłöÈçÏÂÆ”Êę·ÖČŒ±íșÍÍŒËùÊŸ”ÄÆ”Êę·ÖČŒÖ±·œÍŒŁšÆ”Êę·ÖČŒÖ±·œÍŒÖĐÓĐÒ»ŽŠŽíÎóŁ©.
ÇëžùŸĘÍŒ±íĐĆÏą»ŰŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©ÔÚÆ”Êę·ÖČŒ±íÖĐŁŹ![]() ŁŹ
ŁŹ![]() .
.
Łš2Ł©ÖžłöÆ”Êę·ÖČŒÖ±·œÍŒÖДĎíÎóŁŹČąÔÚÉÏžÄŐꣻ
Łš3Ł©ŒŚÍŹŃ§Ë”ŁșĄ°ÎÒ”ÄłÉŒšÊÇŽËŽÎłéŃù”śČéËù”ĂÊęŸĘ”ÄÖĐλÊꥱŁŹÎÊŁșŒŚÍŹŃ§”ÄłÉŒšÓŠÔÚÊČĂŽ·¶Î§Łż
Łš4Ł©È«ÊĐčČÓĐ5000ĂûÆßÄêŒ¶Ń§ÉúŁŹÈôč涚łÉŒšÔÚ80·ÖÒÔÉÏŁšČ»șŹ80·ÖŁ©ÎȘÓĆĐ㣏čÀŒÆŐâŽÎŸșÈüÖĐłÉŒšÎȘÓĆĐă”ÄѧÉúÓжàÉÙÈËŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹĐĄÏïŚóÓÒÁœČàÊÇÊúÖ±”ÄÇœŁŹÒ»ŒÜÌĘŚÓACбżżÔÚÓÒÇœŁŹČâ”ĂÌĘŚÓ¶„¶ËŸàÀë”ŰĂæABŁœ2ĂŚŁŹÌĘŚÓÓë”ŰĂæŒĐœÇŠÁ”ÄŐęÏÒÖ”sinŠÁŁœ0.8ŁźÌĘŚÓ”Ś¶ËλÖĂČ»¶ŻŁŹœ«ÌĘŚÓбżżÔÚŚóǜʱŁŹ¶„¶ËŸàÀë”ŰĂæ2.4ĂŚŁŹÔòĐĄÏï”Äżí¶ÈÎȘ( )
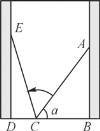
A. 0.7ĂŚB. 1.5ĂŚ
C. 2.2ĂŚD. 2.4ĂŚ
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹ”ăA1ŁŹA2ŁŹA3ŁŹĄ șÍB1ŁŹB2ŁŹB3ŁŹĄ ·Ö±đÔÚÖ±Ïß![]() șÍxÖáÉÏ.ĄśOA1 B1ŁŹĄśB1 A2 B2ŁŹĄśB2 A3 B3ŁŹĄ¶ŒÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁźÈçčû”ăA1(1ŁŹ1)ŁŹÄÇĂŽ”ăA2019”ÄŚĘŚű±êÊÇ( )
șÍxÖáÉÏ.ĄśOA1 B1ŁŹĄśB1 A2 B2ŁŹĄśB2 A3 B3ŁŹĄ¶ŒÊÇ”ÈŃüÖ±œÇÈęœÇĐÎŁźÈçčû”ăA1(1ŁŹ1)ŁŹÄÇĂŽ”ăA2019”ÄŚĘŚű±êÊÇ( )
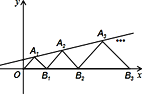
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
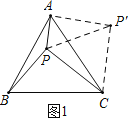
ĄŸÌâÄżĄżŁš1Ł©ÔĶÁÀíœâ:ÀûÓĂĐęŚȘ±ä»»œâŸöÊęѧÎÊÌâÊÇÒ»ÖÖłŁÓÔķœ·šĄŁÈçÍŒŁŹ”ă![]() ÊǔȱßÈęœÇĐÎ
ÊǔȱßÈęœÇĐÎ![]() ÄÚÒ»”㣏
ÄÚÒ»”㣏![]() ŁŹÇó
ŁŹÇó![]() ”ĶÈÊꥣÎȘÀûÓĂÒŃÖȘÌőŒțŁŹČ»·Á°Ń
”ĶÈÊꥣÎȘÀûÓĂÒŃÖȘÌőŒțŁŹČ»·Á°Ń![]() ÈÆ”ă
ÈÆ”ă![]() ËłÊ±ŐëĐęŚȘ60Ąă”Ă
ËłÊ±ŐëĐęŚȘ60Ąă”Ă![]() ŁŹÁŹœÓ
ŁŹÁŹœÓ![]() ŁŹÔò
ŁŹÔò![]() ”Äł€ÎȘ_______Ł»ÔÚ
”Äł€ÎȘ_______Ł»ÔÚ![]() ÖĐŁŹÒŚÖ€
ÖĐŁŹÒŚÖ€![]() ŁŹÇÒ
ŁŹÇÒ![]() ”ĶÈÊęÎȘ_____ŁŹŚÛÉÏżÉ”Ă
”ĶÈÊęÎȘ_____ŁŹŚÛÉÏżÉ”Ă![]() ”ĶÈÊęÎȘ__ Ł»
”ĶÈÊęÎȘ__ Ł»
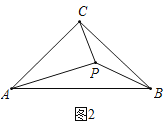
Łš2Ł©Àà±ÈÇšÒÆ:ÈçÍŒŁŹ”ă![]() ÊÇ”ÈŃü
ÊÇ”ÈŃü![]() ÄÚ”ÄÒ»”㣏
ÄÚ”ÄÒ»”㣏![]() ĄŁÇó
ĄŁÇó![]() ”ĶÈÊꣻ
”ĶÈÊꣻ
Łš3Ł©ÍŰŐčÓŠÓĂ:ÈçÍŒŁŹÔÚËıßĐÎ![]() ÖĐŁŹ
ÖĐŁŹ![]() ŁŹÇëÖ±œÓĐŽłö
ŁŹÇëÖ±œÓĐŽłö![]() ”Äł€ĄŁ
”Äł€ĄŁ
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com