
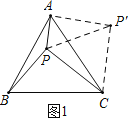
【题目】(1)阅读理解:利用旋转变换解决数学问题是一种常用的方法。如图,点![]() 是等边三角形
是等边三角形![]() 内一点,
内一点,![]() ,求
,求![]() 的度数。为利用已知条件,不妨把
的度数。为利用已知条件,不妨把![]() 绕点
绕点![]() 顺时针旋转60°得
顺时针旋转60°得![]() ,连接
,连接![]() ,则
,则![]() 的长为_______;在
的长为_______;在![]() 中,易证
中,易证![]() ,且
,且![]() 的度数为_____,综上可得
的度数为_____,综上可得![]() 的度数为__ ;
的度数为__ ;
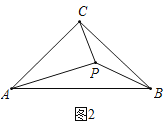
(2)类比迁移:如图,点![]() 是等腰
是等腰![]() 内的一点,
内的一点,![]() 。求
。求![]() 的度数;
的度数;
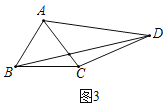
(3)拓展应用:如图,在四边形![]() 中,
中,![]() ,请直接写出
,请直接写出![]() 的长。
的长。
【答案】(1)2, 30°, 90° ;(2)90°;(3)2![]() .
.
【解析】
(1)由旋转性质、等边三角形的判定可知△CP′P是等边三角形,由等边三角形的性质知∠CP′P=60°,根据勾股定理逆定理可得△AP′P是直角三角形,继而可得答案.
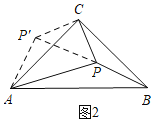
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′,同理可得△CP′P是等腰直角三角形和△AP′P是直角三角形,所以∠APC=90°;
(3)如图3,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,根据勾股定理求CG的长,就可以得BD的长.
解:(1)把△BPC绕点C顺时针旋转60°得△AP'C,连接PP′(如图1).
由旋转的性质知△CP′P是等边三角形;
∴P′A=PB=![]() 、∠CP′P=60°、P′P=PC=2,
、∠CP′P=60°、P′P=PC=2,
在△AP′P中,∵AP2+P′A2=12+(![]() )2=4=PP′2;
)2=4=PP′2;
∴△AP′P是直角三角形;
∴∠P′AP=90°.
∵PA=![]() PC,
PC,
∴∠AP′P=30°;
∴∠BPC=∠CP′A=∠CP′P+∠AP′P=60°+30°=90°.
故答案为:2;30°;90°;
(2)如图2,把△BPC绕点C顺时针旋转90°得△AP'C,连接PP′.
由旋转的性质知△CP′P是等腰直角三角形;
∴P′C=PC=1,∠CPP′=45°、P′P=![]() ,PB=AP'=
,PB=AP'=![]() ,
,
在△AP′P中,∵AP'2+P′P2=(![]() )2+(
)2+(![]() )2=2=AP2;
)2=2=AP2;
∴△AP′P是直角三角形;
∴∠AP′P=90°.
∴∠APP'=45°
∴∠APC=∠APP'+∠CPP'=45°+45°=90°
(3)如图3,
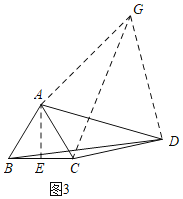
∵AB=AC,
将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,
∵∠BAD=∠CAG,
∴∠BAC=∠DAG,
∵AB=AC,AD=AG,
∴∠ABC=∠ACB=∠ADG=∠AGD,
∴△ABC∽△ADG,
∵AD=2AB,
∴DG=2BC=10,
过A作AE⊥BC于E,
∵∠BAE+∠ABC=90°,∠BAE=∠ADC,
∴∠ADG+∠ADC=90°,
∴∠GDC=90°,
∴CG=![]() =
=![]() =2
=2![]() ,
,
∴BD=CG=2![]() .
.


科目:初中数学 来源: 题型:
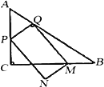
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发,沿折线
出发,沿折线![]() 以每秒
以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动。当点
运动。当点![]() 不与点
不与点![]() 、
、![]() 重合时,在边
重合时,在边![]() 上取一点
上取一点![]() ,满足
,满足![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() ,以
,以![]() 、
、![]() 为边做矩形
为边做矩形![]() .设点
.设点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)当矩形![]() 为正方形时,求
为正方形时,求![]() 的值;
的值;
(3)设矩形![]() 与
与![]() 重叠部分图形的周长为
重叠部分图形的周长为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,作点
,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() .当
.当![]() 、
、![]() 这两点中只有一个点在矩形
这两点中只有一个点在矩形![]() 内部时,直接写出此时
内部时,直接写出此时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等式![]() .
.
![]() 若等式中,已知
若等式中,已知![]() 是非零常量,请写出因变量
是非零常量,请写出因变量![]() 与自变量
与自变量![]() 的函数解析式;当
的函数解析式;当![]() 时,求
时,求![]() 的最大值和最小值及对应的
的最大值和最小值及对应的![]() 的取值.
的取值.
![]() 若等式中,
若等式中,![]() 是非零常量,请写出因变量
是非零常量,请写出因变量![]() 与自变量
与自变量![]() 的函数解析式,并判断
的函数解析式,并判断![]() 在什么范围内取值时,
在什么范围内取值时,![]() 随
随![]() 的增大而增大.
的增大而增大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B(2,0),D(0,3),反比例函数y=![]() (x>0)的图象经过点C.
(x>0)的图象经过点C.
(1)求此反比例函数的解析式;
(2)问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上?
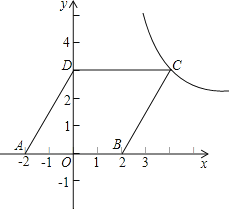
查看答案和解析>>
科目:初中数学 来源: 题型:
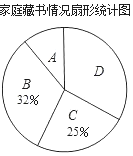
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤100 | a |
C | 101≤m≤200 | 50 |
D | m≥201 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为_____,a=_____;
(2)在扇形统计图中,“A”对应扇形的圆心角为_____°;
(3)若该校有2000名学生,请估计全校学生中家庭藏书200本以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的一个交点坐标是(3,0),对称轴为直线x=1,下列结论:①abc>0;②2a+b=0;③4a﹣2b+c>0;④当y>0时,﹣1<x<3;⑤b<c.其中正确的个数是( )

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
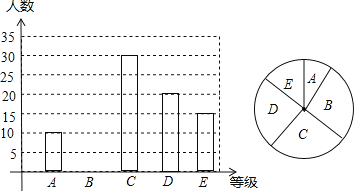
【题目】2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
等级 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
(1)求样本容量及表格中的m和n的值
(2)求扇形统计图中A等级所对的圆心角度数,并补全统计图.
(3)我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
(1)求城门大楼的高度;
(2)每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com