
【题目】如图,在直角坐标系![]() 中,己知
中,己知![]() ,
,![]() ,将线段OA平移至CB,点D在
,将线段OA平移至CB,点D在![]() 轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
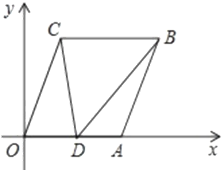
(1)直接写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的2倍时,求点D的坐标;
(3)若∠OCD=25°,∠DBA=15°,求∠BDC.并说明理由.
【答案】(1)C(![]() ,6); (2)点D坐标为(
,6); (2)点D坐标为(![]() ,0)或(
,0)或(![]() ,0);(3)∠CDB=40°.
,0);(3)∠CDB=40°.
【解析】
(1) 延长BC交y轴于点E,由点的坐标的特点,确定出EC、OF的长即可得;
(2)分点D在线段OA和在OA延长线两种情况进行计算;
(3)过点D作DF∥OC,继而由平移的性质可得OC∥AB∥DF,再根据平行线的性质分别求得∠CDF、∠FDB的度数,进而由∠CDB=∠CDF+∠FDB即可求得答案.
(1)如图1,延长BC交y轴于点E,
∵![]() ,将线段OA平移至CB,
,将线段OA平移至CB,
∴BC=OA=![]() ,
,
又∵![]() ,
,
∴BE=![]() ,OE=6,
,OE=6,
∴EC=BE-BC=![]() ,
,
∴C(![]() ,6);
,6);

(2)设D(x,0),当△ODC的面积是△ABD的面积的2倍时,则有OD=2AD,
若点D在线段OA上时,OD=x,AD=![]() -x,
-x,
∵OD=2AD,
∴![]() ×6x=2×
×6x=2×![]() ×6(
×6(![]() ﹣x),
﹣x),
∴x=![]() ,
,
∴D(![]() ,0);
,0);
若点D在线段OA延长线上,OD=x,AD=x-![]() ,
,
∵OD=2AD,
∴![]() ×6x=2×
×6x=2×![]() ×6(x-
×6(x-![]() ),
),
∴x=![]() ,
,
∴D(![]() ,0),
,0),
综上,点D坐标为(![]() ,0)或(
,0)或(![]() ,0);
,0);
(3)如图2.
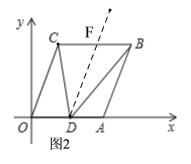
过点D作DF∥OC,
由平移的性质知OC∥AB,
∴OC∥AB∥DF,
∴∠CDF=∠OCD=25°,∠FDB=∠DBA=15°,
∴∠CDB=∠CDF+∠FDB=25°+15°=40°.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
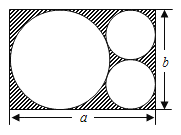
【题目】如图,在一张长为a、宽为b的长方形纸片上,剪掉一个大圆和两个半径相等的小圆.
(1)列出剩余纸片(图中阴影部分)面积的代数式;(结果要求化简)
(2)当a=6cm,b=4cm时,求阴影部分的面积,(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题,例如:∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2).
﹣2).
请解答:(1)![]() 的整数部分是 ,小数部分是
的整数部分是 ,小数部分是
(2)∵2<![]() <3 ,∴1<4-
<3 ,∴1<4- ![]() <2,∴4-
<2,∴4- ![]() 的整数部分是1,小数部分4-
的整数部分是1,小数部分4-![]() -1=3-
-1=3-![]()
已知:9﹣![]() 小数部分是m,9+
小数部分是m,9+![]() 小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值
小数部分是n,且(x+1)2=m+n,请求出满足条件的x的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形ABC中,AB=AC,D、E分别是AC、AB上两点,连结BD、CE,BD=CE,且BC>BD,∠A=48°,∠BCE=36°,则∠ADB的度数等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年10月1日上午,庆祝中华人民共和国成立70周年大会在首都北京天安门广场举行,国庆70年阅兵分列式规模史上最大,共1.5万人参阅,阅兵编59个方(梯)队和联合军乐团,各型飞机160余架,装备580台(套),是近几次阅兵中规模最大的一次.10月1日上午有10万多群众参加游行,10月1日晚上的联欢活动有6万多群众参与,庆祝大会、阅兵式还邀请3万群众参加观礼.这一天参与的群众约19万人,即约190000人,如果参与群众扩大20倍,并且用科学记数法表示,则参与群众约为( )人.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
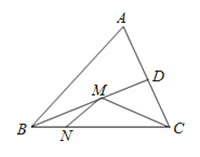
【题目】在锐角△ABC中,∠ABC=60°,BC=2cm,BD平分∠ABC交AC于点D,点M,N分别是BD和BC边上的动点,则MN+MC的最小值是( ).
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC且AB=BC,DE⊥CD且DE=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )

A. 36B. 48C. 72D. 108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了扶贫户学生好读书,读好书,某实验学校校友会在今年开学初,到新华书店采购文学名著和自然科学两类图书.经了解,购买30本文学名著和50本自然科学书共需2350元,20本文学名著比20本自然科学书贵500元.(注:所采购的文学名著价格都一样,所采购的自然科学书价格都一样)
(1)求每本文学名著和自然科学书的单价.
(2)若该校校友会要求购买自然科学书比文学名著多30本,自然科学书和文学名著的总数不低于80本,总费用不超过2400元,请求出所有符合条件的购书方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com