
【题目】把一副三角板按如图放置,其中∠ABC=∠DEB=90°,∠A=45°,∠D=30°,斜边AC=BD=10,若将三角板DEB绕点B逆时针旋转45°得到△D′E′B,则点A在△D′E′B的( ) 
A.内部
B.外部
C.边上
D.以上都有可能
【答案】C
【解析】解:∵AC=BD=10,
又∵∠ABC=∠DEB=90°,∠A=45°,∠D=30°,
∴BE=5,AB=BC=5 ![]() ,
,
由三角板DEB绕点B逆时针旋转45°得到△D′E′B,设△D′E′B与直线AB交于G,可知:∠EBE′=45°,∠E′=∠DEB=90°,
∴△GE′B是等腰直角三角形,且BE′=BE=5,
∴BG= ![]() =5
=5 ![]() ,
,
∴BG=AB,
∴点A在△D′E′B的边上,
故选C.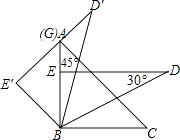
先根据勾股定理求出两直角三角形的各边长,再由旋转的性质得:∠EBE′=45°,∠E′=∠DEB=90°,求出E′D′与直线AB的交点到B的距离也是5 ![]() ,与AB的值相等,所以点A在△D′E′B的边上.本题考查了旋转的性质和勾股定理,利用30°和45°的直角三角形的性质求出各边的长;注意:在直角三角形中,30度角所对的直角边等于斜边的一半,45°角所对的两直角边相等,熟练掌握此内容是解决问题的关键.
,与AB的值相等,所以点A在△D′E′B的边上.本题考查了旋转的性质和勾股定理,利用30°和45°的直角三角形的性质求出各边的长;注意:在直角三角形中,30度角所对的直角边等于斜边的一半,45°角所对的两直角边相等,熟练掌握此内容是解决问题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
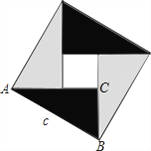
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
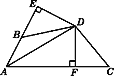
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解该校九年级学生2016年适应性考试数学成绩,现从九年级学生中随机抽取部分学生的适应性考试数学成绩,按A,B,C,D四个等级进行统计,并将统计结果绘制成如图所示不完整的统计图,请根据统计图中的信息解答下列问题:
(说明:A等级:135分﹣150分 B等级:120分﹣135分,C等级:90分﹣120分,D等级:0分﹣90分)
(1)此次抽查的学生人数为;
(2)把条形统计图和扇形统计图补充完整;
(3)若该校九年级有学生1200人,请估计在这次适应性考试中数学成绩达到120分(包含120分)以上的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,AB=8. 
(1)利用尺规,作∠CAB的平分线,交⊙O于点D;(保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD,OD,若AC=CD,求∠B的度数;
(3)在(2)的条件下,OD交BC于点E,求由线段ED,BE, ![]() 所围成区域的面积.(其中
所围成区域的面积.(其中 ![]() 表示劣弧,结果保留π和根号)
表示劣弧,结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF. 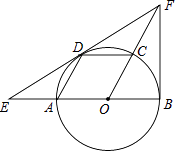
(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“立德树人,志愿服务”活动月中,学校团委为了解本校学生一个月内参加志愿服务次数的情况,随机抽取了部分同学进行统计,并将统计结果分别分成A、B、C、D四类,根据统计结果绘制了如图所示的两幅不完整的统计图.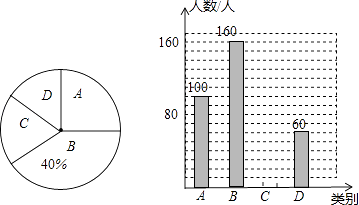
请根据图中信息解答下列问题:
(1)本次抽样调查了名学生,并请补全条形统计图;
(2)被调查学生“一个月内参加志愿服务次数”的人数的众数落在类.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线BD,CE相交于O点,且BD交AC于点D,CE交AB于点E.某同学分析图形后得出以下结论:①![]() BCD≌
BCD≌![]() CBE;②
CBE;②![]() BAD≌
BAD≌![]() BCD;③
BCD;③![]() BDA≌
BDA≌![]() CEA;④
CEA;④![]() BOE≌
BOE≌![]() COD;⑤
COD;⑤ ![]() ACE≌
ACE≌![]() BCE;上述结论一定正确的是
BCE;上述结论一定正确的是

A. ①②③ B. ②③④ C. ①③⑤ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com