
【题目】如图,直线y=﹣3x+3与x轴、y轴分别交于点A、B,抛物线y=a(x﹣2)2+k经过点A、B.求:
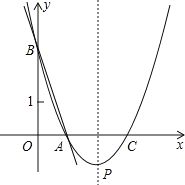
(1)点A、B的坐标;
(2)抛物线的函数表达式;
(3)在抛物线对称轴上是否存在点P,使得以A、B、P为顶点的三角形为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
【答案】(1)A(1,0)、B(0,3).(2)y=(x﹣2)2﹣1.(3)所求的点为P1(2,3),P2(2,3+![]() ),P3(2,3﹣
),P3(2,3﹣![]() ),P4(2,2).
),P4(2,2).
【解析】
试题分析:(1)由y=﹣3x+3得,当x=0时,y=3;当y=0时,x=1,即可确定点A,B的坐标;
(2)把点A(1,0)、B(0,3)代入y=a(x﹣2)2+k得: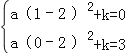 ,解得
,解得![]() ,即可解答;
,即可解答;
(3)存在,由AO=1,BO=3,得到AB=![]() .设对称x轴交于点D,P(2y),D(2,0),所以DA=1,PD=|y|,PA2=PD2+DA2=y2+1,分三种情况讨论解答:当PA=AB即PA2=AB2=10时;当PB=AB即PB2=AB2=10时;当PA=PB即PA2=PB2时.
.设对称x轴交于点D,P(2y),D(2,0),所以DA=1,PD=|y|,PA2=PD2+DA2=y2+1,分三种情况讨论解答:当PA=AB即PA2=AB2=10时;当PB=AB即PB2=AB2=10时;当PA=PB即PA2=PB2时.
解:(1)由y=﹣3x+3得,当x=0时,y=3;当y=0时,x=1
∴A(1,0)、B(0,3).
(2)把点A(1,0)、B(0,3)代入y=a(x﹣2)2+k得:
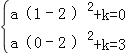
解得![]()
∴抛物线的函数表达式为y=(x﹣2)2﹣1.
(3)∵AO=1,BO=3,
∴AB=![]() .
.
设对称x轴交于点D,P(2,y),D(2,0),
∴DA=1,PD=|y|,PA2=PD2+DA2=y2+1,
当PA=AB即PA2=AB2=10时,
∴y2+1=10,
解得y=±3
∴P(2,±3),
但当P(2,﹣3)时,P、A、B在同一条直线上,不合题意舍去.
∴P1(2,3),
当PB=AB即PB2=AB2=10时,如图,过B作BE⊥对称轴于点E,
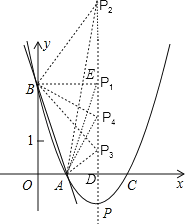
则E(2,3),EB=2,PE2=(y﹣3)2,
∴PB2=PE2+BE2=(y﹣3)2+4=10,
解得![]()
∴P2(2,3+![]() )、P3(2,3﹣
)、P3(2,3﹣![]() ),当PA=PB即PA2=PB2时,
),当PA=PB即PA2=PB2时,
y2+1=(y﹣3)2+4
解得y=2,
∴P4(2,2).
综上所述,所求的点为P1(2,3),P2(2,3+![]() ),P3(2,3﹣
),P3(2,3﹣![]() ),P4(2,2).
),P4(2,2).


科目:初中数学 来源: 题型:
【题目】在一定的条件下,若物体运动的路程s(米)与时间t(秒)的关系式为s=5t2+2t,则当t=4秒时,该物体所经过的路程为( )
A.28米
B.48米
C.68米
D.88米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体内某种细胞的形状可近似看做球状,它的直径是0.00000156m,这个数据用科学记数法可表示为( )
A. 1.56×10﹣6m B. 1.56×10﹣5m C. 156×10﹣5m D. 1.56×106m
查看答案和解析>>
科目:初中数学 来源: 题型:
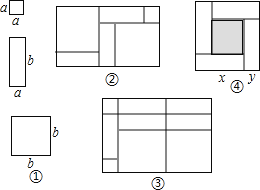
【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的 块, 块, 块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:
(1)![]() (2)x+y=m(3)x2﹣y2=mn(4)
(2)x+y=m(3)x2﹣y2=mn(4)![]()
其中正确的有
A.1个 B.2个 C.3个 D.4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是真命题的个数是( )
①同位角相等;②过一点有且只有一条直线与已知直线垂直;③若a∥b,b∥c,则a∥c;④过直线外一点有且只有一条直线与已知直线平行;⑤三条直线两两相交,总有三个交点.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】森林是地球之肺,每年能为人类提供大约28.3亿吨的有机物.28.3亿吨用科学记数法表示为( )
A.28.3×107
B.2.83×108
C.0.283×1010
D.2.83×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中.
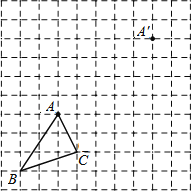
(1)把△ABC平移至A′的位置,使点A与A'对应,得到△A′B′C′;
(2)线段AA′与BB′的关系是: ;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com