
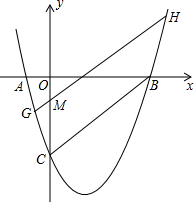
 如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于G、H(G左H右),若点M在y轴上运动,试判断HM-CM的值是否发生变化?若不变化,求出其值;若变化,请说明理由.
如图,抛物线y=x2-2x-3与坐标轴交于A、B、C三点,过y轴上一点M作BC的平行线交抛物线于G、H(G左H右),若点M在y轴上运动,试判断HM-CM的值是否发生变化?若不变化,求出其值;若变化,请说明理由. 分析 作HE⊥y轴于E,GF⊥y轴于F,如图,先解方程x2-2x-3=0得到A(-1,0),B(3,0),计算自变量为0时的函数值得到C(0,-3),则△OBC为等腰直角三角形,再利用GH∥BC判断△GMF和△EMH都为等腰直角三角形,所以HM=$\sqrt{2}$HE,GM=$\sqrt{2}$GF,则HM-GM=$\sqrt{2}$(HE-GF),易得直线BC的解析式为y=x-3,可设直线GH的解析式为y=x+k,利用二次函数图象与直线的交点问题,若设H、G点的横坐标分别为a、b,则a、b为方程x2-2x-3=x+k的两根,根据根与系数的关系得到a+b=3,而HE=a,GF=-b,HM-GM=$\sqrt{2}$(HE-GF)=$\sqrt{2}$(a+b)=3$\sqrt{2}$,即HM-GM的值不发生变化.
解答 解:HM-GM的值不发生变化.
作HE⊥y轴于E,GF⊥y轴于F,如图,
当y=0时,x2-2x-3=0,解得x1=-1,x2=3,则A(-1,0),B(3,0),
当x=0时,y=x2-2x-3=-3,则C(0,-3),
∵OB=OC=3,
∴△OBC为等腰直角三角形,
∴∠OCB=45°
∵GH∥BC,
∴∠GMF=∠EMH=45°,
∴△GMF和△EMH都为等腰直角三角形,
∴HM=$\sqrt{2}$HE,GM=$\sqrt{2}$GF,
∴HM-GM=$\sqrt{2}$(HE-GF),
易得直线BC的解析式为y=x-3,由于GH∥BC,则可设直线GH的解析式为y=x+k,
设H、G点的横坐标分别为a、b,则a、b为方程x2-2x-3=x+k的两根,
方程整理为x2-3x-3-k=0,
∴a+b=3,
∵HE=a,GF=-b,
∴HM-GM=$\sqrt{2}$(HE-GF)=$\sqrt{2}$(a+b)=3$\sqrt{2}$,
即HM-GM的值不发生变化.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决本题的关键把HM-GM的值转化为点H与点G的横坐标和的$\sqrt{2}$倍.


科目:初中数学 来源:2016-2017学年江苏省扬州市七年级下学期第一次月考数学试卷(解析版) 题型:填空题
将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是__________.

查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:判断题
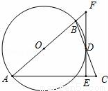
如图,△ABC中,AB=AC,作以AB为直径的⊙O与边BC交于点D,过点D作⊙O的切线,分别交AC、AB的延长线于点E、F.
(1)求证:EF⊥AC;
(2)若BF=2,CE=1.2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
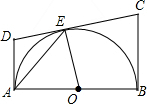 如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( )
如图,AB是⊙O的直径,DA,DC,BC都是⊙O的切线,切点为A、E、B,若DC=9,AD=4,则BC的长为( )| A. | 9 | B. | 6 | C. | 5 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲、乙两船同时从小岛O出发,甲船速度为40海里/时,沿北偏西20°的方向航行;乙船沿北偏东70°的方向,以30海里/时的速度航行,半小时后甲、乙两船分别到达A,B两处.
甲、乙两船同时从小岛O出发,甲船速度为40海里/时,沿北偏西20°的方向航行;乙船沿北偏东70°的方向,以30海里/时的速度航行,半小时后甲、乙两船分别到达A,B两处.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com