
【题目】为了解市民对“雾霾天气的主要原因”的认识,某调查公司随机抽查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
组别 | 观点 | 频数(人数) |
| 大气气压低,空气不流动 | 100 |
| 底面灰尘大,空气湿度低 |
|
| 汽车尾气排放 |
|
| 工厂造成的污染 | 140 |
| 其他 | 80 |
调查结果扇形统计图

请根据图表中提供的信息解答下列问题:
(1)填空:![]() __________,
__________,![]() __________.扇形统计图中
__________.扇形统计图中![]() 组所占的百分比为__________%.
组所占的百分比为__________%.
(2)若该市人口约有100万人,请你估计其中持![]() 组“观点”的市民人数约是__________万人.
组“观点”的市民人数约是__________万人.
(3![]() 组“观点”的概率是__________.
组“观点”的概率是__________.
科目:初中数学 来源: 题型:
【题目】如图,一条城际铁路从A市到B市需要经过C市,A市位于C市西南方向,与C市相距40在千米,B市恰好位于A市的正东方向和C市的南偏东60°方向处.因打造城市经济新格局需要,将从A市到B市之间铺设一条笔直的铁路,求新铺设的铁路AB的长度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与⊙O的位置关系,并说明理由;
(2)若BD=2![]() ,BF=2,求阴影部分的面积(结果保留π).
,BF=2,求阴影部分的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
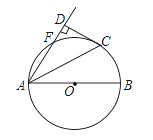
【题目】如图,AB是⊙O的直径,点F、C在⊙O上且![]() , 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
, 连接AC、AF,过点C作CD⊥AF交AF的延长线于点D.
(1)求证:CD是⊙O的切线;
(2)若![]() , CD=4,求⊙O的半径.
, CD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
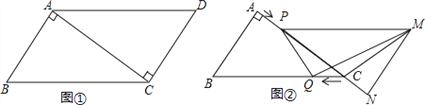
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的网格图中,每小格都是边长为1的正方形,△ABC的三个顶点都在格点上,在建立直角坐标系后,点C的坐标(-1,2)
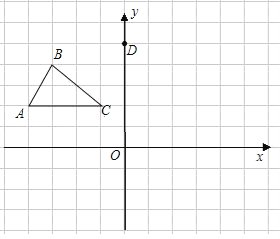
(1)画出△ABC绕点D(0,5)逆时针旋转90°后的△A1B1C1,
(2)写出A1,C1的坐标.
(3)求点A旋转到A1所经过的路线长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表中所列x,y的数值是某二次函数y=ax2+bx+c图象上的点所对应的坐标,其中x1<x2<x3<x4<x5<x6<x7 , 根据表中所提供的信息,以下判断正确的是( ).
①a>0;②9<m<16;③k≤9;④b2≤4a(c﹣k).
x | … | x1 | x2 | x3 | x4 | x5 | x6 | x7 | … |
y | … | 16 | m | 9 | k | 9 | m | 16 | … |
A. ①② B. ③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,F,G是直径AB上的两点,C,D,E是半圆上的三点,如果弧AC的度数为60°,弧BE的度数为20°,∠CFA=∠DFB,∠DGA=∠EGB.求∠FDG的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com