
【题目】如图,在四边形ABCD中,AD∥BC,F在CD上,且AF垂直平分CD,FG平分∠AFD,交AD于G,连接GB,交AF于N,且FN=FD.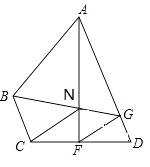
(1)求证:△GFN≌△GFD;
(2)如图,连接ND,若BC=ND,∠ADC=75°,求证:AN=AB;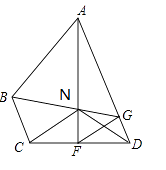
(3)如图2,延长AF、BC交于点E,过B作BK⊥AE于K,若∠BAF=2∠E,猜想,AB与KF之间有何数量关系?请说明理由.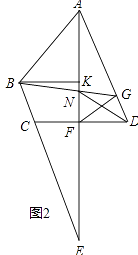
【答案】
(1)
证明:∵FG平分∠AFD,
∴∠NFG=∠GFD,
在△GFN和△GFD中, 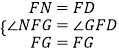 ,
,
∴△GFN≌△GFD(SAS)
(2)
证明:连接AC,如图1所示:
∵AF⊥CD,FN=FD,
∴△DFN为等腰直角三角形,
∴∠FDN=45°,
∵∠ADC=75°,
∴∠ADN=∠ADC﹣∠FDN=75°﹣45°=30°,
在Rt△AFD中,∠FAD=90°﹣75°=15°
∵AF垂直平分CD,
∴AC=AD,
∴∠ACD=∠ADC=75°,
∴∠CAD=30°,
∵AD∥BC,
∴∠BCA=∠CAD=30°,
∴∠ADN=∠BCA,
在△ADN和△ACB中, 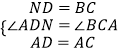 ,
,
∴△ADN≌△ACB(SAS),
∴AN=AB
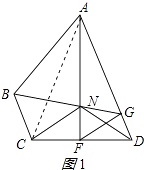
(3)
解:AB与KF之间有何数量关系为:AB=2KF;理由如下:
取AB中点H,连接HF、HK,如图2所示:
∵在Rt△AKB中,H为AB中点,
∴HK= ![]() AB=AH,
AB=AH,
∴∠HAK=∠HKA,
∵∠BAF=2∠E,
∴∠HKA=2∠E,
∵AD∥BE,
∴△AFD∽△EFC,
∴ ![]() =
= ![]() =1,
=1,
∴AF=EF,
∵H为AB中点,
∴HF为△ABE的中位线,
∴HF∥BE,
∴∠HFK=∠E,
∴∠HKA=2∠HFK,
∵∠HKA=∠HFK+∠FHK,
∴2∠HFK=∠HFK+∠FHK,
∴∠HFK=∠FHK,
∴HK=KF,
∵HK= ![]() AB,
AB,
即AB=2HK,
∴AB=2KF.
【解析】(1)由角平分线得出∠NFG=∠GFD,由SAS证明△GFN≌△GFD即可;(2)连接AC,由等腰直角三角形的性质得出∠FDN=45°,由线段垂直平分线的性质得出AC=AD,证出∠CAD=30°,由SAS证明△ADN≌△ACB,得出对应边相等即可;(3)取AB中点H,连接HF、HK,由直角三角形斜边上的中线性质得出HK= ![]() AB=AH,得出∠HAK=∠HKA,证明△AFD∽△EFC,得出对应边成比例,证出AF=EF,证明HF为△ABE的中位线,由三角形中位线定理得出HF∥BE,得出∠HFK=∠E,由角的关系得出∠HFK=∠FHK,得出HK=KF,即可得出结论.
AB=AH,得出∠HAK=∠HKA,证明△AFD∽△EFC,得出对应边成比例,证出AF=EF,证明HF为△ABE的中位线,由三角形中位线定理得出HF∥BE,得出∠HFK=∠E,由角的关系得出∠HFK=∠FHK,得出HK=KF,即可得出结论.


科目:初中数学 来源: 题型:
【题目】一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB, 改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值 . 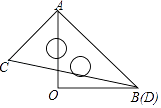
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x、y的二元一次方程组![]() 给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )
给出下列结论:①当k=5时,此方程组无解;②若此方程组的解也是方程6x+15y=16的解,则k=10;③无论整数k取何值,此方程组一定无整数解(x、y均为整数),其中正确的是( )
A.①②③
B.①③
C.②③
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·齐齐哈尔中考)矩形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件________________,使其成为正方形(只填一个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣3交x轴于B、C两点,且B的坐标为(﹣2,0)直线y=mx+n过点B和抛物线上另一点A(4,3)
(1)求抛物线和直线的解析式;
(2)若点P为抛物线上的一个动点,且在直线AB下方,过P作PQ∥x轴,且PQ=4(点Q在P点右侧).以PQ为一边作矩形PQEF,且点E在直线AB上.求矩形PQEF的最大值.并求出此时点P的坐标;
(3)如图2,在(2)的结论下,连接AP、BP,设QE交于x轴于点D,现即将矩形PQEF沿射线DB以每秒1个单位长度的速度平移,当点D到达点B时停止,记平移时间为t,平移后的矩形PQEF为P′Q′E′F′,且Q′E′分别交直线AB、x轴于N、D′,设矩形P′Q′E′F′与△ABP的重叠部分面积为s,当NA= ![]() ND′时,求s的值.
ND′时,求s的值.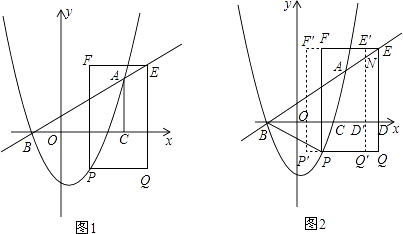
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com