
【题目】某蔬菜专业户试种植了一种紧俏蔬菜(都能卖出),其中每千克的成本![]() 在9元/千克的基础上,还有一些上浮.若浮动价(元/
在9元/千克的基础上,还有一些上浮.若浮动价(元/![]() )与需求量
)与需求量![]() (千克)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价
(千克)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价![]() (元/
(元/![]() )与市场需求量
)与市场需求量![]() 有如下关系:
有如下关系:
需求量 | 50 | 40 | 30 | 20 |
蔬菜售价 | 10 | 15 | 20 | 25 |
(1)直接写出每千克的成本![]() 与需求量
与需求量![]() 的关系式_________;
的关系式_________;
(2)求![]() 与
与![]() 的关系式;
的关系式;
(3)当某天的利润率达到![]() 时,求这天的需求量;
时,求这天的需求量;
(4)求需求量是多少千克时,利润达到最大值,最大值是多少?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)30千克或4千克;(4)当26千克时取得最大利润是308元
;(3)30千克或4千克;(4)当26千克时取得最大利润是308元
【解析】
(1)先根据题意表示出浮动价(元/![]() )与需求量
)与需求量![]() (千克)的反比例函数关系再加上成本价9元即可.
(千克)的反比例函数关系再加上成本价9元即可.
(2)观察图表可发现蔬菜售价![]() (元/
(元/![]() )与市场需求量
)与市场需求量![]() 为一次函数关系,设其解析式
为一次函数关系,设其解析式![]() ,代入两点解答即可.
,代入两点解答即可.
(3)利润率达到![]() ,其关系表示即为
,其关系表示即为![]() ,将两函数表达式代入转化为关于
,将两函数表达式代入转化为关于![]() 的方程解答即可.
的方程解答即可.
(4)将利润表示为关于市场需求量![]() 的二次函数关系式,用配方法求最值即可.
的二次函数关系式,用配方法求最值即可.
解:(1)![]()
(2)观察发现需求量每减少10千克,蔬菜售价会增加5元/![]() ,是一次函数关系
,是一次函数关系
设![]() ,把
,把![]() 和
和![]() 代入得
代入得
![]()
解得: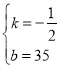
则![]()
(3)法1:每天的利润![]()
每天的总成本:![]()
当![]() 时,
时,![]()
整理得:![]()
![]() ,
,![]()
法2:∵利润率![]()
∴![]()
![]() 整理得
整理得![]() ,
,
∴![]() ,
,![]()
经检验![]() ,
,![]() 是原方程的解
是原方程的解
(4)![]()
![]()
因为![]()
所以函数有最大值,当![]() 时取得最大利润,为308元.
时取得最大利润,为308元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“爱心”帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共9千顶,现某地震灾区急需帐篷14千顶,该集团决定在一周内赶制出这批帐篷.为此,全体职工加班加点,总厂和分厂一周内制作的帐篷数分别达到了原来的1.6倍、1.5倍,恰好按时完成了这项任务.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶?
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的![]() 两地,由于两市通住
两地,由于两市通住![]() 两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
|
| ||
每千顶帐篷 所需车辆数 | 甲市 | 4 | 7 |
乙市 | 3 | 5 | |
所急需帐篷数(单位:千顶) | 9 | 5 | |
请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() +bx+c与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OC=2OA=2,点D是直线BC下方抛物线上一动点.
+bx+c与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OC=2OA=2,点D是直线BC下方抛物线上一动点.
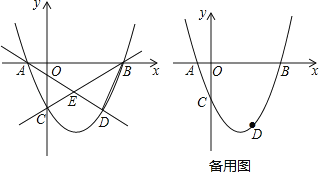
(1)求出抛物线的解析式;
(2)连接AD和BC,AD交BC于点E,当S△ABE:S△BDE=5:4时,求点D的坐标;
(3)点F为y轴上的一点,在(2)的条件下,求DF+![]() OF的最小值.
OF的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在推进郑州市城乡生活垃圾分类的行动中,某社区对居民掌握垃圾分类知识的情况进行调査.其中![]() ,
,![]() 两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
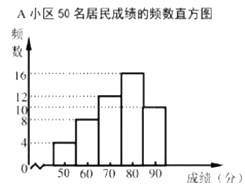
(信息二)上图中,从左往右第四组的成绩如下:
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() ,
,![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 | 40% | 277 | |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数.
小区50名居民成绩的中位数.
(2)请估计![]() 小区1000名居民成绩能超过平均数的人数.
小区1000名居民成绩能超过平均数的人数.
(3)请尽量从多个角度(至少三个),选择合适的统计量分析![]() ,
,![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别是某函数图象与
分别是某函数图象与![]() 轴、
轴、![]() 轴的交点,点
轴的交点,点![]() 是此图象上的一动点.设点
是此图象上的一动点.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的长为
的长为![]() ,且
,且![]() 与
与![]() 之间满足关系:
之间满足关系:![]() ,则正确结论的序号是( )
,则正确结论的序号是( )
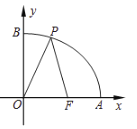
①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() ;④
;④![]() 的最大值是6.
的最大值是6.
A.①②③B.③④C.①②④D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的.连接BE、CF相交于点D.
(1)求证:BE=CF.
(2)当四边形ACDE为菱形时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线![]() 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为
上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为![]()
![]()
A. 3 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知第一象限内的点
中,已知第一象限内的点![]() 在反比例函数y=
在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,连接
的图象上,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 的图象上的一点,过点
的图象上的一点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .点
.点![]() 为
为![]() 轴正半轴上的一点,连接
轴正半轴上的一点,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() .若
.若![]() ,且
,且![]() 的面积为18,则
的面积为18,则![]() 的值是( )
的值是( )
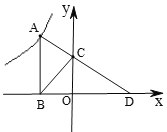
A.6B.-6C.12D.-12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com