
【题目】如图,抛物线y=![]() +bx+c与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OC=2OA=2,点D是直线BC下方抛物线上一动点.
+bx+c与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,且OC=2OA=2,点D是直线BC下方抛物线上一动点.
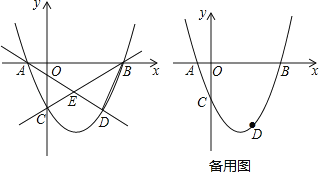
(1)求出抛物线的解析式;
(2)连接AD和BC,AD交BC于点E,当S△ABE:S△BDE=5:4时,求点D的坐标;
(3)点F为y轴上的一点,在(2)的条件下,求DF+![]() OF的最小值.
OF的最小值.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣2;(2)D(2,﹣3);(3)
x﹣2;(2)D(2,﹣3);(3)![]()
【解析】
(1)OC=2OA=2,则点A、C的坐标分别为:(-1,0)、(0,-2),则c=-2,将点A的坐标代入抛物线表达式,即可求解;
(2)S△ABE:S△BDE=5:4,则AE:ED=5:4,AM∥HD,则AM:HD=AE:ED=5:4,则HD=2,即可求解;
(3)作一条与y轴夹角为α的直线AH,使tan∠HOF=![]() =tanα,则sin
=tanα,则sin![]() ,过点D作DH⊥AH交AH于点H,交y轴于点F,则点F为所求点,即可求解.
,过点D作DH⊥AH交AH于点H,交y轴于点F,则点F为所求点,即可求解.
(1)OC=2OA=2,
则点A、C的坐标分别为:(﹣1,0)、(0,﹣2),
则c=﹣2,
将点A的坐标代入抛物线表达式并解得:b=﹣![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣2;
x﹣2;
(2)由点B、C的坐标得,直线BC的表达式为:y=![]() x﹣2,
x﹣2,
S△ABE:S△BDE=5:4,则AE:ED=5:4,
分别过点A、D作y轴的平行线分别交BC于点M、H,

∴AM∥HD,当x=﹣1时,y=![]() x﹣2=﹣
x﹣2=﹣![]() ,
,
∵AM∥HD,∴AM:HD=AE:ED=5:4,
∴HD=2,
设点D(x,![]() x2﹣
x2﹣![]() x﹣2),则点H(x,
x﹣2),则点H(x,![]() x﹣2),
x﹣2),
DH=![]() x﹣2﹣(
x﹣2﹣(![]() x2﹣
x2﹣![]() x﹣2)=2,解得:x=2,
x﹣2)=2,解得:x=2,
故点D(2,﹣3);
(3)作一条与y轴夹角为α的直线AH,使tan∠HOF=![]() =tanα,则sin
=tanα,则sin![]() ,
,
过点D作DH⊥AH,交AH于点H,交y轴于点F,则点F为所求点,
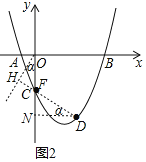
DF+![]() OF=FD+HF最小,
OF=FD+HF最小,
过点D作x轴的平行线交y轴于点N,则∠FDN=α,
则直线FD的表达式为:y=﹣![]() x+n,
x+n,
将点D的坐标代入上式并解得:
直线DF的表达式为:y=﹣![]() x﹣
x﹣![]() ,故点F(0,﹣
,故点F(0,﹣![]() ),
),
则OF=![]() ,
,
DF+![]() OF的最小值=FD+HF=
OF的最小值=FD+HF=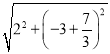 +
+![]() ×
×![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校现有九年级学生800名,为了了解这些学生的体质健康情况,学校在开学初从中随机抽取部分学生进行体能测试(测试结果分成优秀、良好、合格、不合格四个等级),并将测试结果绘制成如图所示两幅不完整的统计图,请结合图中提供的信息解答下列问题:
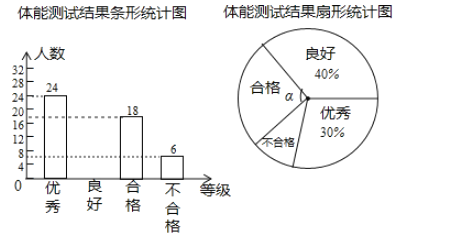
(1)本次抽取的学生人数共有____名,在扇形统计图中,“合格”等级所对应的圆心角![]() 的度数是______;
的度数是______;
(2)补全条形统计图;
(3)估计九年级学生中达到“合格”以上(含合格)等级的学生一共有多少名?
(4)若抽取的学生中,恰好有九年级(1)班的2名男生,2名女生,现要从这4人中随机抽取2人担任组长工作,请用列表法或树状图法求所抽取的2名学生中至少有1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD在直线MN的上方,BC在直线MN上,E是BC上一点,以AE为边在直线MN的上方作正方形AEFG.
(1)连接GD,求证:△ADG≌△ABE;
(2)连接FC,观察并猜测∠FCN的度数,并说明理由;
(3)如图(2),将图(1)中正方形ABCD改为矩形ABCD,AB=a,BC=b(a、b为常数),E是线段BC上一动点(不含端点B、C),以AE为边在直线MN的上方作矩形AEFG,使顶点G恰好落在射线CD上.判断当点E由B向C运动时,∠FCN的大小是否总保持不变?若∠FCN的大小不变,请用含a、b的代数式表示tan∠FCN的值;若∠FCN的大小发生改变,请举例说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标是A(0,﹣2),B(6,﹣4),C(2,﹣6).
(1)请画出与△ABC关于x轴对称的△A1B1C1.
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴左侧画出△A2B2C2.
,得到△A2B2C2,请在y轴左侧画出△A2B2C2.
(3)在y轴上存在点P,使得△OB2P的面积为6,请直接写出满足条件的点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月26日第5届中国国际大数据产业博览会召开.某市在五届数博会上的产业签约金额的折线统计图如图.下列说法正确的是( )

A. 签约金额逐年增加
B. 与上年相比,2019年的签约金额的增长量最多
C. 签约金额的年增长速度最快的是2016年
D. 2018年的签约金额比2017年降低了22.98%
查看答案和解析>>
科目:初中数学 来源: 题型:
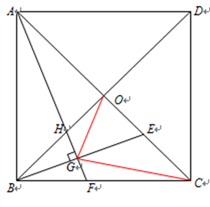
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交B0于H,连接OG,CC.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜专业户试种植了一种紧俏蔬菜(都能卖出),其中每千克的成本![]() 在9元/千克的基础上,还有一些上浮.若浮动价(元/
在9元/千克的基础上,还有一些上浮.若浮动价(元/![]() )与需求量
)与需求量![]() (千克)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价
(千克)成反比,比例系数为30.市场连续四天调查发现,蔬菜售价![]() (元/
(元/![]() )与市场需求量
)与市场需求量![]() 有如下关系:
有如下关系:
需求量 | 50 | 40 | 30 | 20 |
蔬菜售价 | 10 | 15 | 20 | 25 |
(1)直接写出每千克的成本![]() 与需求量
与需求量![]() 的关系式_________;
的关系式_________;
(2)求![]() 与
与![]() 的关系式;
的关系式;
(3)当某天的利润率达到![]() 时,求这天的需求量;
时,求这天的需求量;
(4)求需求量是多少千克时,利润达到最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费由两部分组成:固定费用400元和服务费用5元/平方米;
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.
(1)求甲公司养护费用y(元)与绿化面积x(平方米)的函数解析式(不要求写出自变量的范围);
(2)选择哪家公司的服务,每月的绿化养护费用较少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com