【题目】如图，已知
为
三边垂直平分线的交点，且
，则
的度数为（ ）
A.
B.
C.
D.
【答案】B
【解析】
延长AO交BC于D，根据垂直平分线的性质可得到AO=BO=CO，再根据等边对等角的性质得到∠OAB=∠OBA，∠OAC=∠OCA，再由三角形的外角性质可求得∠BOD=∠OAB+∠OBA，∠COD=∠OAC+∠OCA，从而不难求得∠BOC的度数．
延长AO交BC于D．
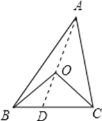
∵点O在AB的垂直平分线上．
∴AO=BO．
同理：AO=CO．
∴∠OAB=∠OBA，∠OAC=∠OCA．
∵∠BOD=∠OAB+∠OBA，∠COD=∠OAC+∠OCA．
∴∠BOD=2∠OAB，∠COD=2∠OAC．
∴∠BOC=∠BOD+∠COD=2∠OAB+2∠OAC=2（∠OAB+∠OAC）=2∠BAC．
∵∠A=50°．
∴∠BOC=100°．
故选：B．
手拉手全优练考卷系列答案科目：初中数学 来源： 题型：
【题目】通过对下面数学模型的研究学习，解决下列问题：
（模型呈现）（1）如图1，
，
，过点
作
于点
，过点
作
于点
.由
，得
.又
，可以推理得到
.进而得到
，
.我们把这个数学模型称为“
字”模型或“一线三等角”模型；
（模型应用）（2）①如图2，
，，
，连接
，
，且
于点
，与直线
交于点
是的中点；
②如图3，在平面直角坐标系
中，点
的坐标为
，点为平面内任一点.若
是以
为斜边的等腰直角三角形，请直接写出点的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
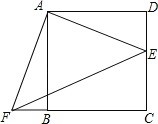
【题目】如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转△ABF的位置．
（1）旋转中心是点 ，旋转角度是 度；
（2）若连结EF，则△AEF是 三角形；并证明；
（3）若四边形AECF的面积为25，DE=2，求AE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC＞60°，∠BAC＜60°，以AB为边作等边△ABD（点C、D在边AB的同侧），连接CD．
（1）若∠ABC
90°，∠BAC
30°，求∠BDC的度数；
（2）当∠BAC
2∠BDC时，请判断△ABC的形状并说明理由；
（3）当∠BCD等于多少度时，∠BAC
2∠BDC恒成立．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在等边三角形
中，
为
边上的高.
操作发现:（1）如图1，过点
分别作
，
，垂足分别为
.请直接写出
和的数量关系；
（2）如图2，若点
为上任意一点（不与
重合），过点作
，
，垂足分别为.判断
和的数量关系，并说明理由；
拓广探索:（3）如图3，点为等边三角形内任意一点，过点作
，，，垂足分别为
，探究
和的数量关系，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在如图所示的正方形网格中，每个小正方形的边长都是1，已知三角形
的三个顶点的坐标分别为
，
，
（1）作出三角形关于
轴对称的三角形
（2）点
的坐标为 .
（3）①利用网络画出线段
的垂直平分线
；②
为直线上上一动点，则
的最小值为 .
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是半圆的直径，点O是圆心，点C是OA的中点，CD⊥OA交半圆于点D，点E是
的中点，连接AE、OD，过点D作DP∥AE交BA的延长线于点P．
（1）求∠AOD的度数；
（2）求证：PD是半圆O的切线．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数
（
，
是常数，
）的图象过
，
两点.
（1）在图中画出该一次函数并求其表达式；
（2）若点
在该一次函数图象上，求
的值；
（3）把的图象向下平移3个单位后得到新的一次函数图象，在图中画出新函数图形，并直接写出新函数图象对应的表达式.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在等边三角形ABC中，点D在线段AB上，点E在CD的延长线上，连接AE，AE=AC，AF平分∠EAB，交CE于点F，连接BF.
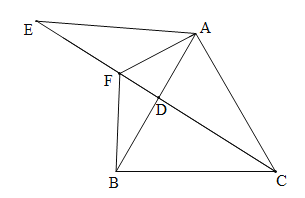
（1）求证：EF=BF；
（2）猜想∠AFC的度数，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com