Question

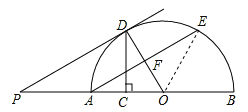
【题目】如图，AB是半圆的直径，点O是圆心，点C是OA的中点，CD⊥OA交半圆于点D，点E是的中点，连接AE、OD，过点D作DP∥AE交BA的延长线于点P．

（1）求∠AOD的度数；

（2）求证：PD是半圆O的切线．

Answer 1

【答案】（1）解：∵点C时OA的中点，∴OC=OA=OD

∵CD⊥OA，∴∠OCD=90°。

在Rt△OCD中，cos∠COD=

∴∠COD=60°，即∠AOD=60°。

（2）证明：连结OE，∵点E是的中点，

∴，

∴∠BOE=∠DOE=∠DOB=（180°-∠COD）=（180°-60°）=60°。

∵OA=OE，∴∠EAO=∠AEO，又∠EAO+∠AEO=∠EOB=60°

∴∠EAO=30°，

∴PD∥AE，

∴∠P=∠EAO=30°。

由（1）知∠AOD=60°，∴∠PDO=180°-（∠P+∠POD）=180°-（30°+60°）=90°，

∴PD是半圆O的切线。

【解析】

试题（1）根据CO与DO的数量关系，即可得出∠CDO的度数，进而求出∠AOD的度数；

（2）利用点E是的中点，进而求出∠EAB=30°，即可得出∠AFO=90°，即可得出答案．

试题解析：（1）∵AB是半圆的直径，点O是圆心，点C是OA的中点，

∴2CO=DO，∠DCO=90°，

∴∠CDO=30°，

∴∠AOD=60°；

（2）如图，连接OE，

∵点E是的中点，

∴，

∵由（1）得∠AOD=60°，

∴∠DOB=120°，

∴∠BOE=60°，

∴∠EAB=30°，

∴∠AFO=90°，

∵DP∥AE，

∴PD⊥OD，

∴直线PD为⊙O的切线．