
分析 设出直线与x轴的交点坐标和与y轴交点坐标,表示出三角形的周长,根据(a-b)2≥0,a2+b2≥2ab,确定周长取最小值时a与b的关系,求出周长的最小值.
解答 解:设直线与x轴的交点A为(a,0),与y轴交点B为(0,b),
则△AOB的周长为:a+b+$\sqrt{{a}^{2}+{b}^{2}}$
根据(a-b)2≥0,a2+b2≥2ab,
所以当a=b时,周长有最小值,
因为直线经过点(2,1),
a=b=3
周长的最小值为2$\sqrt{ab}$+$\sqrt{2ab}$=6+3$\sqrt{2}$.
点评 本题考查的是一次函数图象上点的坐标的特征,解题的关键是根据完全平方的非负性,确定周长取最小值时a与b的关系,进行解答.


科目:初中数学 来源: 题型:填空题
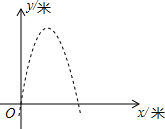 滕州市政府大楼前广场有一喷水池,喷出水的路径是一条抛物线,如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空号总划出的曲线是抛物线y=-x2+6x(单位:米)的一部分,则水喷出的最大高度是9米.
滕州市政府大楼前广场有一喷水池,喷出水的路径是一条抛物线,如果以水平地面为x轴,建立如图所示的平面直角坐标系,水在空号总划出的曲线是抛物线y=-x2+6x(单位:米)的一部分,则水喷出的最大高度是9米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D.则∠ADB的度数为100°.
如图,在△ABC中,∠ACB=80°,∠ABC=60°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧相交于点G;③作射线AG交BC于点D.则∠ADB的度数为100°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com