
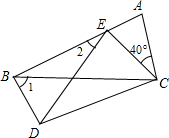
 如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )
如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )| A、90° | B、100° |
| C、110° | D、120° |
科目:初中数学 来源: 题型:
 甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以2a千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
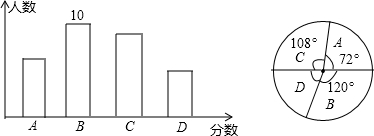 某校组织学生绘画比赛,对参赛作品按A、B、C、D四个等级进行评定:四个等级的分数分别为A级5分,B级4分,C级2分,D级1分.现随机抽取部分学生绘画作品的评定结果进行分析,并绘制如下条形图和扇形统计图,根据图中信息,这些学生的平均分数是( )
某校组织学生绘画比赛,对参赛作品按A、B、C、D四个等级进行评定:四个等级的分数分别为A级5分,B级4分,C级2分,D级1分.现随机抽取部分学生绘画作品的评定结果进行分析,并绘制如下条形图和扇形统计图,根据图中信息,这些学生的平均分数是( )| A、3.0 | B、3.1 |
| C、3.2 | D、3.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、0个 | B、1个 | C、2个 | D、3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一次函数y=
如图,一次函数y=| 3 |
| 4 |
| 24 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com