
|
|


科目:初中数学 来源: 题型:
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、了解浙江卫视《中国好声音-The Voice of China》的收视率情况适合用抽样调查 | ||||
| B、在一个只装有白球和红球的袋中摸球,摸出黑球是不确定事件 | ||||
| C、今年3月份某周,我市每天的最高气温(单位:℃)分别是12,9,10,6,11,12,17,则这组数据的极差是5℃ | ||||
D、如果甲组数据的方差
|
查看答案和解析>>
科目:初中数学 来源: 题型:
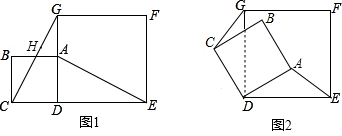
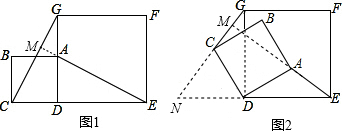
 直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=4
直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=4| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
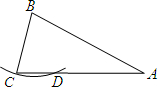 如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )
如图,在△ABC中,AB=AC=2BC,以点B为圆心,BC长为半径作弧,与AC交于点D.若AC=4,则线段CD的长为( )A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
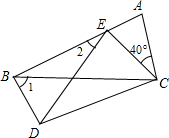 如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )
如图,四边形ABDC中,△EDC是由△ABC绕顶点C旋转40°所得,顶点A恰好转到AB上一点E的位置,则∠1+∠2=( )| A、90° | B、100° |
| C、110° | D、120° |
查看答案和解析>>
科目:初中数学 来源: 题型:
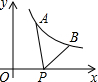 如图,已知点A(1,y1)、B(2,y2)是反比例函数y=
如图,已知点A(1,y1)、B(2,y2)是反比例函数y=| 2 |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com