
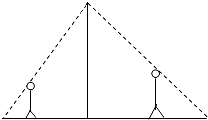
 如图,小明和他的父亲晚饭后到广场去散步,休息时小明站在广场中电灯的左侧,距离电灯支杆的距离为3米,影长为1米,小明的父亲站在电灯的右侧,他距离电灯支杆的距离为4.3米.已知小明的身高为1.5米,小明父亲身高为1.7米,则此时小明父亲的影长为多少米?
如图,小明和他的父亲晚饭后到广场去散步,休息时小明站在广场中电灯的左侧,距离电灯支杆的距离为3米,影长为1米,小明的父亲站在电灯的右侧,他距离电灯支杆的距离为4.3米.已知小明的身高为1.5米,小明父亲身高为1.7米,则此时小明父亲的影长为多少米? 分析 根据相似三角形的判定与性质得出$\frac{CB}{CZ}=\frac{AB}{QZ}$,$\frac{FG}{ZG}$=$\frac{EF}{QZ}$,进而求出FG的长即可得出答案.
解答 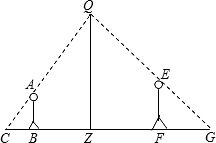 解:根据已知得出:
解:根据已知得出:
AB∥DZ∥EF,
∴$\frac{CB}{CZ}=\frac{AB}{QZ}$,$\frac{FG}{ZG}$=$\frac{EF}{QZ}$,
∵AB=1.5m,EF=1.7m,FG=1.7m,BZ=3,ZF=4.3,BC=1,
∴$\frac{1}{1+3}$=$\frac{1.5}{QZ}$,
∴QZ=6m
∴$\frac{FG}{FG+4.3}=\frac{1.7}{6}$,
∴FG=1.7.
故答案为:1.7.
点评 此题主要考查了相似三角形的判定与性质,根据已知得出三角形对应边之间的关系是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
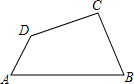 如图,在四边形ABCD的边AB上任取一点O(不与点A、B重合)连接OC、OD,分别取OA、OB、OC、OD的中点A′、B′、C′、D′,连接A′D′、D′C′、C′B′、,四边形A′B′C′D′与四边形ABCD相似吗?为什么?
如图,在四边形ABCD的边AB上任取一点O(不与点A、B重合)连接OC、OD,分别取OA、OB、OC、OD的中点A′、B′、C′、D′,连接A′D′、D′C′、C′B′、,四边形A′B′C′D′与四边形ABCD相似吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com