练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．直角三角形斜边上的中线长为5，斜边上的高是4，直角三角形的面积是20．

    分析 根据直角三角形的斜边上中线性质求出斜边的长，再根据三角形的面积公式求出即可．

    解答 解：
    ∵CD是Rt△ACB斜边AB上的中线，
    ∴AB=2CD=2×5=10，
    ∴Rt△ACB的面积S=$\frac{1}{2}$AB×CE=$\frac{1}{2}$×4×10=20．
    故答案是：20．

    点评 本题考查了直角三角形斜边上中线性质的应用，解此题的关键是根据性质求出AB的长，注意：直角三角形斜边上的中线等于斜边的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．如图，将一张正方形纸片剪去四个大小形状一样的小正方形，然后将其中一个小正方形再按同样的方法剪成四个小正方形，再将其中一个小正方形剪成四个小正方形，再将其中的一个小正方形剪成四个小正方形，如此循环进行下去．
    （1）填表：
    剪的次数12345
    正方形个数47101316
    （2）如果剪了100次，共剪出多少个小正方形？
    （3）如果剪n次，共剪出多少个小正方形？
    （4）如果要剪出100个正方形，那么需要剪多少次？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图，是一个10×10的正方形网格，其中正方形的顶点称为格点，网格中△ABC的顶点A，B，C均在格点上，利用网格建立的平面直角坐标系中点A的坐标为（3，4）．
    （1）直接写出B，C两点的坐标：B（1，2）；C（5，1）；
    （2）将A，B，C三点的纵坐标保持不变，横坐标分别乘-1，得到点A1，B1，C1，在图中描出点A1，B1，C1，并画出△A1B1C1；
    （3）描述图中的△A1B1C1与△ABC的位置关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，有一个形如六边形的点阵，它的中心是一个点，算第一层；第二层每边有两个点，第三层每边有三个点，依此类推．
    （1）填写表：
    层数1234…
    该层对应的点数161218…
    所有层的总点数171937…
    （2）写出第n层所对应的点数．
    （3）如果某一层有96个点，请计算它是第几层？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，AB是⊙O的直径，点P在⊙O上，若弦BD=3，sinP=$\frac{3}{5}$，求⊙O的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．一木工师傅有两根长分别为80cm、150cm的木条，他要找第三根木条，将它们钉成一个三角形框架，他可以选择长为（　　）的木条．
    A．70cmB．105cmC．230cmD．300

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图1，点O为直线AB上一点，过点O作射线OC，使∠BOC=120°，将有一30度角的直角三角板的直角顶点放在点O处，一边OM在射线OB上，另一边ON在直线AB的下方．（图中∠OMN=30°，∠NOM=90°）

    （1）将图1中的三角板绕点O逆时针旋转至图2，使OM在∠BOC的内部，且恰好平分∠BOC，问直线ON是否平分∠AOC？请说明理由；
    （2）将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线ON恰好平分锐角∠AOC，求t；
    （3）将图1中的三角板绕点O顺时针旋转至图3，使ON在∠AOC的内部，请探究：∠AOM与∠NOC之间的数量关系，并说明理由．

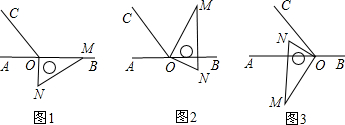
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

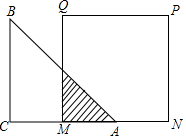    19．如图，已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为10cm，AC与MN在同一直线上，开始时点A与点M重合，让△ABC向右移动，最后让点A与点N重合．
    （1）试写出重叠部分面积y（cm2）与线段MA的长度x（cm）之间的函数解析式；
    （2）写出自变量的取值范围；
    （3）写出当x=4时重叠部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列说法错误的是（　　）
    A．已知两边及一角只能作出唯一的三角形
    B．到△ABC的三个顶点距离相等的点是△ABC的三条边垂直平分线的交点
    C．腰长相等的两个等腰直角三角形全等
    D．点A（3，2）关于x轴的对称点A坐标为（3，-2）

    查看答案和解析>>

    同步练习册答案