
【题目】如图,![]() 内的线段
内的线段![]() 、
、![]() 相交于点
相交于点![]() ,已知
,已知![]() ,
,![]() ,则
,则![]() 是__________.
是__________.

【答案】![]()
【解析】
连接AO,利用等高不等底的三角形面积比等于底边长的比,可表示出△AOC与△COD的面积.根据S△BOE+S△AOE=S△AOCS△COD,即可表示出四边形AEOD的面积.
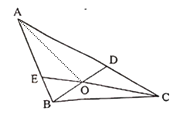
解:连接OA,设△BOE和△AOE的面积分别为m、n,
∴OC=2OE,
∴2S△BOE=S△BOC=2m,
∵OB=OD,
∴S△BOC=S△COD=2m,
∵OC=2OE,
∴2S△AOE=S△AOC=2n,
∵OB=OD,
∴S△AOB=S△AOD=m+n,
∴S△BOE+S△AOE=S△AOCS△COD,即:m+n=2n2m,
∴n=3m,
∵S四边形AEOD=S△AOE+S△AOD=n+m+n=m+2n=7m,
∴![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
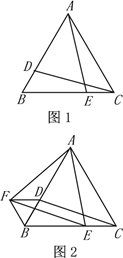
【题目】如图1,图2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图1所示的位置时,求证:CD=AE.
(2)把图1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图2),分别连结DF、EF.
①找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
②试判断四边形CDFE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的课外活动,学校决定购进5副羽毛球拍和![]() 只羽毛球,已知一副羽毛球拍的价格是一只羽毛球的价格的15倍,用50元可以买一副羽毛球拍和10只羽毛球;
只羽毛球,已知一副羽毛球拍的价格是一只羽毛球的价格的15倍,用50元可以买一副羽毛球拍和10只羽毛球;
(1)一副羽毛球拍和一只羽毛球的价格各是多少元?
(2)甲乙两商店举行促销活动,甲商店给出的优惠是:所有商品打八折;乙商店的优惠是:买一副羽毛球拍送![]() 只羽毛球:通过调查发现,如果只到一个商店购买5副羽毛球拍和26只羽毛球时,到甲商店更划算;若只购买一副羽毛球拍和
只羽毛球:通过调查发现,如果只到一个商店购买5副羽毛球拍和26只羽毛球时,到甲商店更划算;若只购买一副羽毛球拍和![]() 只羽毛球,则乙商店更划算。求
只羽毛球,则乙商店更划算。求![]() 的值;
的值;
(3)在(2)的条件下,当![]() 时,学校购买这批羽毛球拍和羽毛球最少需要元(直接写出结果).
时,学校购买这批羽毛球拍和羽毛球最少需要元(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同时抛掷A,B两个均匀的小立方体(每个面上分别标有数字1,2,3,4,5,6),设两立方体朝上的数字分别为x,y,并以此确定点P(x,y),那么点P落在直线y=-2x+9上的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将x=![]() 代入反比例函数y=-
代入反比例函数y=-![]() 中,所得的函数值记为
中,所得的函数值记为![]() ,又将x=
,又将x=![]() +1代入反比例函数y=-
+1代入反比例函数y=-![]() 中,所得的函数值记为
中,所得的函数值记为![]() ,又将x=
,又将x=![]() +1代入反比例函数y=-
+1代入反比例函数y=-![]() 中,所得的函数值记为
中,所得的函数值记为![]() ,…,如此继续下去,则y2020=______________
,…,如此继续下去,则y2020=______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:(1)如图,已知:在等腰直角![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() 直线
直线![]() ,
,![]() 直线
直线![]() ,垂足分别为点
,垂足分别为点![]() 、
、![]() .小明观察图形特征后猜想线段
.小明观察图形特征后猜想线段![]() 、
、![]() 和
和![]() 之间存在
之间存在![]() 的数量关系,请你判断他的猜想是否正确,并说明理由.
的数量关系,请你判断他的猜想是否正确,并说明理由.

(2)如图,将(1)中的条件改为:![]() 为等边三角形,
为等边三角形,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上,并且有
上,并且有![]() ,请问结论
,请问结论![]() 是否成立?并说明理由.
是否成立?并说明理由.

(3)如图,若将(1)中的三角形变形为一般的等腰三角形,![]() 中,
中,![]() ,
,![]() ,其中
,其中![]() 为任意锐角或钝角,
为任意锐角或钝角,![]() 、
、![]() 、
、![]() 三点都在直线
三点都在直线![]() 上.问:满足什么条件时,结论
上.问:满足什么条件时,结论![]() 仍成立?直接写出条件即可.
仍成立?直接写出条件即可.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆汽车和一辆摩托车分别从A,B两地去同一城市,l1 ,l2分别表示汽车、摩托车离A地的距离s(km)随时间t(h)变化的图象,则下列结论:①摩托车比汽车晚到1 h;②A,B两地的距离为20 km;③摩托车的速度为45 km/h,汽车的速度为60 km/h;④汽车出发1 h后与摩托车相遇,此时距离B地40 km;⑤相遇前摩托车的速度比汽车的速度快.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com