Question

【题目】如图，Rt△ABC中，∠ACB=90°，CD是斜边AB上的高，角平分线AE交CD于H， EF⊥AB于F，下列结论：
①∠ACD=∠B；②CH=CE=EF；③AC=AF；④CH=HD．
其中正确的结论为（ ）

A.①②④
B.①②③
C.②③
D.①③

Answer 1

【答案】B
【解析】解：∵∠B和∠ACD都是∠CAB的余角， ∴∠ACD=∠B，故①正确；
∵CD⊥AB，EF⊥AB，
∴EF∥CD，
∴∠AEF=∠CHE，
∴∠CEH=∠CHE，
∴CH=CE=EF，故②正确；
∵角平分线AE交CD于H，
∴∠CAE=∠BAE，
在△ACE和△AEF中， ，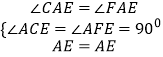
∴△ACE≌△AFE（AAS），
∴AC=AF，故③正确；
CH=CE=EF＞HD，
故④错误．
故正确的结论为①②③．
故选B．
根据等角的余角相等可判断①；先判断CD∥EF，根据平行线的性质得出∠CEH=∠CHE，再由角平分线的性质可判断②；用AAS判定△ACE≌△AFE，可判断③；根据②，结合图形可判断④．