
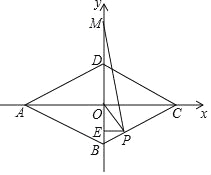
【题目】以菱形![]() 的对角线交点
的对角线交点![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,已知
轴,已知![]() ,
,![]() ,
,![]() ,
,![]() 为折线
为折线![]() 上一动点,内行
上一动点,内行![]() 轴于点
轴于点![]() ,设点
,设点![]() 的纵坐标为
的纵坐标为![]()
(1)求![]() 边所在直线的解析式;
边所在直线的解析式;
(2)设![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)当![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标.
的坐标.
【答案】(1)直线BC的解析式为y=![]() x﹣2;
x﹣2;
(2)当点P在边BC上时, y=10a2+24a+48;
当点P在边CD上时,y= 10a2﹣40a+48;
(3)点P的坐标为(![]() ,2﹣
,2﹣![]() ),(4,0).
),(4,0).
【解析】
试题分析:(1)先确定出OA=4,OB=2,再利用菱形的性质得出OC=4,OD=2,最后用待定系数法即可确定出直线BC解析式;
(2)分两种情况,先表示出点P的坐标,利用两点间的距离公式即可得出函数关系式;
(3)分两种情况,利用勾股定理的逆定理建立方程即可求出点P的坐标.
试题解析:(1)∵A(﹣4,0),B(0,﹣2),∴OA=4,OB=2,
∵四边形ABCD是菱形,∴OC=OA=4,OD=OB=2,∴C(4,0),D(0,2),
设直线BC的解析式为y=kx﹣2,∴4k﹣2=0,∴k=![]() ,∴直线BC的解析式为y=
,∴直线BC的解析式为y=![]() x﹣2;
x﹣2;
(2)由(1)知,C(4,0),D(0,2),∴直线CD的解析式为y=﹣![]() x+2,
x+2,
由(1)知,直线BC的解析式为y=![]() x﹣2,
x﹣2,
当点P在边BC上时,设P(2a+4,a)(﹣2≤a<0),
∵M(0,4),
∴y=MP2+OP2=(2a+4)2+(a﹣4)2+(2a+4)2+a2=2(2a+4)2+(a﹣4)2+a2=10a2+24a+48
当点P在边CD上时,
∵点P的纵坐标为a,
∴P(4﹣2a,a)(0≤a≤2),
∵M(0,4),∴y=MP2+OP2=(4﹣2a)2+(a﹣4)2+(4﹣2a)2+a2=10a2﹣40a+48,
(3)①当点P在边BC上时,即:0≤a≤2,
由(2)知,P(2a+4,a),
∵M(0,4),∴OP2=(2a+4)2+a2=5a2+16a+16,PM2=(2a+4)2+(a﹣4)2=5a2﹣8a+32,OM2=16,
∵△POM是直角三角形,易知,PM最大,
∴OP2+OM2=PM2,
∴5a2+16a+16+16=5a2﹣8a+32,
∴a=0(舍)
②当点P在边CD上时,即:0≤a≤2时,
由(2)知,P(4﹣2a,a),
∵M(0,4),
∴OP2=(4﹣2a)2+a2=5a2﹣16a+16,PM2=(4﹣2a)2+(a﹣4)2=5a2﹣24a+32,OM2=16,
∵△POM是直角三角形,
Ⅰ、当∠POM=90°时,
∴OP2+OM2=PM2,
∴5a2﹣16a+16+16=5a2﹣24a+32,
∴a=0,
∴P(4,0),
Ⅱ、当∠MPO=90°时,OP2+PM2=5a2﹣16a+16+5a2﹣24a+32=10a2﹣40a+48=OM2=16,
∴a=2+![]() (舍)或a=2﹣
(舍)或a=2﹣![]() ,
,
∴P(![]() ,2﹣
,2﹣![]() ),
),
即:当△OPM为直角三角形时,点P的坐标为(![]() ,2﹣
,2﹣![]() ),(4,0).
),(4,0).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AN是⊙M的直径,NB∥x轴,AB交⊙M于点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:直线CD是⊙M的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图14,![]() 是
是![]() 的直径,
的直径,![]() ,连接
,连接![]() .
.
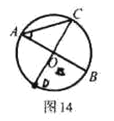
(1)求证:![]() ;
;
(2)若直线![]() 为
为![]() 的切线,
的切线,![]() 是切点,在直线
是切点,在直线![]() 上取一点
上取一点![]() ,使
,使![]() 所在的直线与
所在的直线与![]() 所在的直线相交于点
所在的直线相交于点![]() ,连接
,连接![]() .
.
①试探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
②![]() 是否为定值?若是,请求出这个定值;若不是,请说明理由.
是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,菱形ABCD中,对角线AC,BD相交于点O,若再补充一个条件能使菱形ABCD成为正方形,则这个条件是 . (只填一个条件即可,答案不唯一) 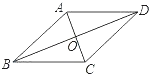
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某报纸公布的我国“九五”期间国内生产总值(GDP)的统计表,那么这几年间我国国内生产总值平均每年比上一年增长___万亿元.
年份 | 1996 | 1997 | 1998 | 1999 | 2000 |
GDP/万亿元 | 6.6 | 7.3 | 7.9 | 8.2 | 8.9 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个. 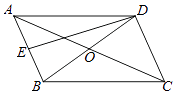
A.3
B.4
C.5
D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com