
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a﹣b+c,则P的取值范围是( ) 
A.﹣4<P<0
B.﹣4<P<﹣2
C.﹣2<P<0
D.﹣1<P<0
【答案】A
【解析】解:∵二次函数的图象开口向上, ∴a>0,
∵对称轴在y轴的左边,
∴﹣ ![]() <0,
<0,
∴b>0,
∵图象与y轴的交点坐标是(0,﹣2),过(1,0)点,
代入得:a+b﹣2=0,
∴a=2﹣b,b=2﹣a,
∴y=ax2+(2﹣a)x﹣2,
当x=﹣1时,y=a﹣b+c=a﹣(2﹣a)﹣2=2a﹣4,
∵b>0,
∴b=2﹣a>0,
∴a<2,
∵a>0,
∴0<a<2,
∴0<2a<4,
∴﹣4<2a﹣4<0,
∵y=a﹣b+c=a﹣(2﹣a)﹣2=2a﹣4,
∴﹣4<a﹣b+c<0,
即﹣4<P<0.
故选:A.
【考点精析】解答此题的关键在于理解二次函数图象以及系数a、b、c的关系的相关知识,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c).


科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE= ![]() AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.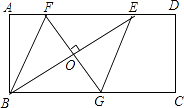
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1 , 矩形ABCD的面积为S2 , 当 ![]() =
= ![]() 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以图1(以O为圆心,半径1 的半圆)作为“基本图形”,分别经历如下变换能得到图2的序号是 (多填或错填得0分,少填酌情给分)
①只要向右平移1个 单位;
② 先以直线AB为对称轴进行对称变换,再向右平移1个单位;
③先绕着O旋转180°,再向右平移1个单位;
④只要绕着某点旋转180°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,AC=4 cm,BC=3 cm,将三角形ABC沿AB方向向右平移得到三角形DEF,若AE=8 cm,DB=2 cm.
(1)求三角形ABC向右平移的距离AD的长;
(2)求四边形AEFC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应我市“中国梦”“宜宾梦”主题教育活动,某中学在全校学生中开展了以“中国梦我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.小明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
等级 | 频数 | 频率 |
一等奖 | a | 0.1 |
二等奖 | 10 | 0.2 |
三等奖 | b | 0.4 |
优秀奖 | 15 | 0.3 |
请你根据以上图表提供的信息,解答下列问题:
(1)a= , b= , n= .
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一节”前,某商场用60万元购进某种商品,该商品有甲、乙两种包装共500件,其中每件甲包装中有75个A种产品,每个A产品的成本为12元;每件乙包装中有100个B产品,每个B种产品的成本为14元.商场将A产品标价定为每个18元,B产品标价定为每个20元.
(1)甲、乙两种包装的产品各有多少件?
(2)“五一节”商场促销,将A产品按原定标价打9折销售,B种产品按原定标价打8.5折销售,“五一节”期间该产品全部卖完,该商场销售该商品共获利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com