
【题目】如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE2=AB ![]() CF;③CF=
CF;③CF= ![]() FD; ④△ABE∽△AEF.其中正确的有( )
FD; ④△ABE∽△AEF.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】因为正方形ABCD中,E是BC的中点,所以tan∠BAE= ![]() ,所以∠BAE≠30°,故①错误;因为∠BAE+∠BEA=90°,∠BEA+∠CEF=90°;所以∠BAE=∠CEF,又因为∠B=∠C=90°,所以△ABE∽△ECF则AB:BE=EC:CF,因为BE=CE,所以AB:CE=EC:CF,即CE2=AB
,所以∠BAE≠30°,故①错误;因为∠BAE+∠BEA=90°,∠BEA+∠CEF=90°;所以∠BAE=∠CEF,又因为∠B=∠C=90°,所以△ABE∽△ECF则AB:BE=EC:CF,因为BE=CE,所以AB:CE=EC:CF,即CE2=AB ![]() CF,所以②正确;
CF,所以②正确;
设CF=a,则BE=CE=2a,AB=CD=AD=4a,DF=3a,∴AE=2 ![]() a,EF=
a,EF= ![]() a,AF=5a,∴
a,AF=5a,∴ ![]() ,
, ![]() ,∴
,∴ ![]() ,∴△ABE∽△AEF,故④正确.∴CF=
,∴△ABE∽△AEF,故④正确.∴CF= ![]() EC=
EC= ![]() CD,∴CF=
CD,∴CF= ![]() FD;故③正确;所以答案是:C.
FD;故③正确;所以答案是:C.
【考点精析】利用相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,两艘海监船刚好在某岛东西海岸线上的A、B两处巡逻,同时发现一艘不明国籍船只停在C处海域,AB=60( ![]() +1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.
+1)海里,在B处测得C在北偏东45°反向上,A处测得C在北偏西30°方向上,在海岸线AB上有一灯塔D,测得AD=100海里.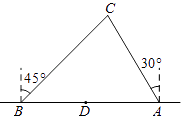
(1)分别求出AC,BC(结果保留根号).
(2)已知在灯塔D周围80海里范围内有暗礁群,在A处海监穿沿AC前往C处盘查,途中有无触礁的危险?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).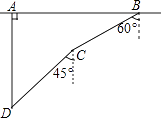
查看答案和解析>>
科目:初中数学 来源: 题型:
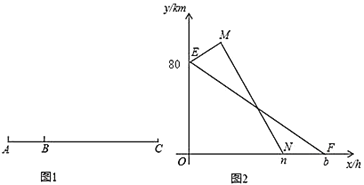
【题目】如图有A、B、C三地依次在一条笔直的公路上,A、B两地相距40km,一辆甲车以40km/h的速度从B地到C地;同时一辆乙车以80km/h的速度从B地开往A地,到达A地后,然后以120km/h的速度开往C地,两车在各段内均匀速行驶,图中线段EF与折线EMN分别表示甲、乙两车距C地的路程y(千米)与行驶时间x(小时)之间的函数关系图象.
(1)写出点M的坐标为_______;点E的纵坐标的意义是________.
(2)请直接写出n,b的值,并求出线段EF与MN的函数关系式;
(3)两车出发几小时后,乙车追上甲车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.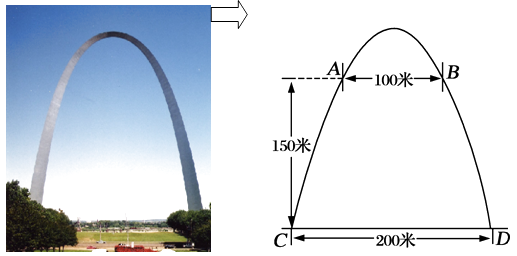
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形纸片ABCD的边长为3,点E,F分别在边BC、CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都落在点G处,已知BE=1,则EF的长为( )
A.1.5
B.2.5
C.2.25
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,连接BD,点O是BD的中点,若M,N是边AD上的两点,连接MO,NO,并分别延长交边BC于两点M′,N′,则图中的全等三角形共有( )
A.2对
B.3对
C.4对
D.5对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com