
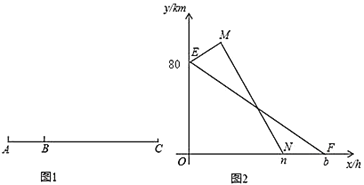
����Ŀ����ͼ��A��B��C����������һ����ֱ�Ĺ�·�ϣ�A��B�������40km��һ���׳���40km/h���ٶȴ�B�ص�C�أ�ͬʱһ���ҳ���80km/h���ٶȴ�B�ؿ���A�أ�����A�غ�Ȼ����120km/h���ٶȿ���C�أ������ڸ����ھ�������ʻ��ͼ���߶�EF������EMN�ֱ��ʾ�ס���������C�ص�·��y(ǧ��)����ʻʱ��x(Сʱ)֮��ĺ�����ϵͼ��
(1)д����M������Ϊ_______����E���������������________.
(2)��ֱ��д��n��b��ֵ��������߶�EF��MN�ĺ�����ϵʽ��
(3)����������Сʱ���ҳ��ϼ׳���
���𰸡�(1)(![]() ��120)��B�㵽C��ľ�����80km��(2)n=
��120)��B�㵽C��ľ�����80km��(2)n=![]() ��b=2���߶�EF�ĺ�����ϵʽ��
��b=2���߶�EF�ĺ�����ϵʽ��![]() ���߶�MN�ĺ�����ϵʽ��
���߶�MN�ĺ�����ϵʽ��![]() ��(3)
��(3)![]() Сʱ.
Сʱ.
��������
��1��������ҳ���B�ؿ���A������ʱ�䣬���ɵõ�M�����ꣻ�������֪��E���������������B�㵽C��ľ�����80km����2��nΪ�ҳ���B�ؿ���A���ٿ���C������ʱ�䣬bΪ�׳���B�ص�C�ص�ʱ�䣬�ʿɽ�����⣬�ó�M,N,F�����꣬���ɸ��ݴ���ϵ����ȷ��������ϵʽ����3������������ȣ������������������.
��1���ҳ���B�ؿ���A������ʱ��Ϊ![]() h������C��120km,
h������C��120km,
��M��![]() ��120����
��120����
��E���������������B�㵽C��ľ�����80km��
��2��nΪ�ҳ���B�ؿ���A���ٿ���C������ʱ�䣬��n=![]() +
+![]() =
=![]() ����N(
����N(![]() ,0)
,0)
bΪ�׳���B�ص�C�ص�ʱ��,��b=![]() ����F��2,0��
����F��2,0��
���߶�EFΪy=k1x+b1,����E��0,80����F(2��0)����߶�EF�ĺ�����ϵʽ��![]() ��
��
���߶�MNΪy=k2x+b2,����M��![]() ��120����N(
��120����N(![]() ,0)����߶�EF�ĺ�����ϵʽ��
,0)����߶�EF�ĺ�����ϵʽ��![]() ,
,
��3����![]() =
=![]()
���x=![]()
����������![]() Сʱ���ҳ��ϼ׳�.
Сʱ���ҳ��ϼ׳�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ���������س���չ�����ijУ���־���Χ���ڡ��赸�����������֡�Ϸ�������������Ŀ�У�����ϲ����һ����ÿ��ֻ��һ������⣬��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬������������������������������ͳ��ͼ���������ͳ��ͼ����������⣺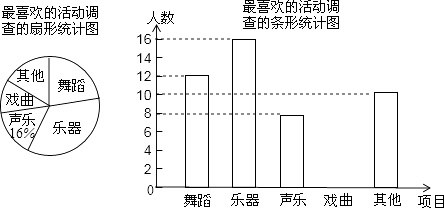
��1������ε����У�һ���������ѧ��������ϲ�����赸�����Ŀ������ռ����������İٷֱ�Ϊ �� ����ͳ��ͼ��ϲ����Ϸ�����������ε�Բ�Ľ�Ϊ�ȣ�
��2�����㲹ȫ����ͳ��ͼ��
��3�����ڡ��赸�����������֡�Ϸ������Ŀ����ѡ�������������ȤС�飬�����б�����״ͼ�ķ�����ǡ��ѡ�С��赸�����֡�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ϰ�ȥͼ�������г�����ij��ͼ�飬��һ����1200Ԫ�������ɱ����������鶨��7Ԫ���ۣ��ܿ����꣮���ڸ��鳩�����ڶ��ι���ʱ��ÿ������������ѱȵ�һ�������20%������1500Ԫ��������������ȵ�һ�ζ�10�������������۳�200��ʱ���������������Զ��۵�4������ʣ����飮
(1)��һ�ι���Ľ����Ƕ���Ԫ��
(2)���ʸ��ϰ���������������������Ǯ�ˣ�����Ǯ��(��������������)������Ǯ������٣���Ǯ�����٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y=kx+b�뷴��������y= ![]() ��x��0����ͼ����A��m��6����B��3��n������
��x��0����ͼ����A��m��6����B��3��n������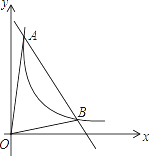
��1����һ�κ����Ľ���ʽ��
��2������ͼ��ֱ��д��ʹkx+b�� ![]() ������x��ȡֵ��Χ��
������x��ȡֵ��Χ��
��3�����AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ij�̵�����һ�����ͽ��ܵƣ�ÿյ���ܵƽ���Ϊ18Ԫ�����������з��֣�ÿ������y��յ�������۵���x��Ԫ��֮���ϵ���Խ��Ƶؿ���һ�κ���y=��2x+100��������=�ۼ۩����ۣ�
��1��д��ÿ�ܵ�����w��Ԫ�������۵���x��Ԫ��֮�亯������ʽ��
��2�������۵��۶�Ϊ����Ԫʱ�����ֽ��ܵ�ÿ���ܹ�������������������Ƕ���Ԫ��
��3����۲��Ź涨�����ֽ��ܵƵ����۵��۲��ø���30Ԫ�����̵���Ҫ���ֽ��ܵ�ÿ�ܻ��350Ԫ�����������۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����������ABCD�У�E��BC���е㣬F��CD�ϵ�һ�㣬AE��EF�����н��ۣ��١�BAE��30�㣻��CE2��AB ![]() CF����CF��
CF����CF�� ![]() FD�� �ܡ�ABE�ס�AEF.������ȷ���У� ��
FD�� �ܡ�ABE�ס�AEF.������ȷ���У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�����������100ǧ�ף��ּƻ��������м�����һ�����ٹ�·�����߶�AB������������ɭ�ֱ���������P�����A���еı�ƫ��30��ķ����ϣ�����B���е���ƫ��45��ķ����ϣ���֪ɭ�ֱ������ķ�Χ����PΪԲ�ģ�35ǧ��Ϊ�뾶��Բ�������ڣ����ʣ��ƻ��������������ٹ�·��ᴩԽɭ�ֱ���������ͨ������˵�������ο����ݣ� ![]() ��1.732��
��1.732�� ![]() ��1.414��
��1.414��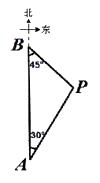
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ǵȱ������Σ���D��ֱ��BC��һ�㣬��ADΪһ����AD���Ҳ����ȱ�
�ǵȱ������Σ���D��ֱ��BC��һ�㣬��ADΪһ����AD���Ҳ����ȱ�![]() ��
��
![]() ��ͼ
��ͼ![]() ����D���߶�BC���ƶ�ʱ��ֱ��д��
����D���߶�BC���ƶ�ʱ��ֱ��д��![]() ��
��![]() �Ĵ�С��ϵ��
�Ĵ�С��ϵ��
![]() ��ͼ
��ͼ![]() ͼ
ͼ![]() ����D���߶�BC���ӳ����ϻ����ӳ������ƶ�ʱ������
����D���߶�BC���ӳ����ϻ����ӳ������ƶ�ʱ������![]() �Ĵ�С�Ƿ����仯����������ֱ��д�����۲�ѡ������һ��ͼʾ����֤�������仯����ֱ�д��ͼ
�Ĵ�С�Ƿ����仯����������ֱ��д�����۲�ѡ������һ��ͼʾ����֤�������仯����ֱ�д��ͼ![]() ��ͼ
��ͼ![]() ����Ӧ�Ľ��ۣ�
����Ӧ�Ľ��ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���
��1���������������ͼ1����ABC�ǵȱ������Σ���D���߶�AB�ϣ���E��ֱ��BC�ϣ��ҡ�DEC=��DCE����֤��BE=AD��
��2�������ѧϰ����ͼ2������������D���߶�AB�ϡ���Ϊ����D���߶�AB���ӳ����ϡ��������������䣮�ж��߶�AB��BE��BD֮���������ϵ����˵�����ɣ�
��3������չ̽������ͼ3����ABC�ǵ��������Σ�AB=AC����BAC=120�㣬��D���߶�AB�ķ����ӳ����ϣ���E��ֱ��BC�ϣ��ҡ�DEC=��DCE�������ѧϰ���е��߶�AB��BE��BD֮���������ϵ�Ƿ���������������˵�����ɣ�������������ֱ��д���߶�AB��BE��BD֮���������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com