
【题目】永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价)
(1)写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元?
(3)物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元?
【答案】
(1)解:w=(x﹣18)y=(x﹣18)(﹣2x+100)
=﹣2x2+136x﹣1800,
∴z与x之间的函数解析式为z=﹣2x2+136x﹣1800(x>18)
(2)解:∵w=﹣2x2+136x﹣1800=﹣2(x﹣34)2+512,
∴当x=34时,w取得最大,最大利润为512万元.
答:当销售单价为34元时,厂商每周能获得最大利润,最大利润是512万元.
(3)解:周销售利润=周销量×(单件售价﹣单件制造成本)=(﹣2x+100)(x﹣18)=﹣2x2+136x﹣1800,
由题意得,﹣2x2+136x﹣1800=350,
解得:x1=25,x2=43,
∵销售单价不得高于30元,
∴x取25,
答:销售单价定为25元时厂商每周能获得350万元的利润;
【解析】(1)根据利润w=(每盏节能灯的售价-每盏节能灯的进价)![]() 每周的销量y,即可求出函数解析式。
每周的销量y,即可求出函数解析式。
(2)将(1)中的函数解析式通过配方,求出其顶点坐标,即可得出结果。
(3)此小题的等量关系是:每周获得的利润w=350,建立方程求解即可。注意:0<x≤30.
【考点精析】本题主要考查了因式分解法和二次函数的最值的相关知识点,需要掌握已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势;如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y= ![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )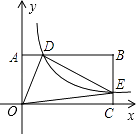
A.![]()
B.![]()
C.![]()
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,三个内角的平分线交于点
中,三个内角的平分线交于点![]() ,过点
,过点![]() 作
作![]() ,交边
,交边![]() 于点
于点![]() .
.
(1)如图,若∠ABC=40°,则∠AOC= ,∠ADO= ;
(2)猜想![]() 与
与![]() 的关系,并说明你的理由;
的关系,并说明你的理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
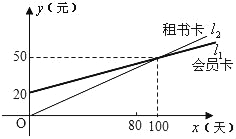
【题目】某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租一本书,租书金额y(元)与租书时间x(天)之间的关系如图所示:
(1)用租书卡每天租书的收费为 元,用会员卡每天租书的收费是 元;
(2)分别写出用租书卡和会员卡租书的金额y1、y2与租书时间x之间的函数关系式;
(3)如果租书50天,选择哪种租书方式比较划算?如果花费80元租书,选择哪种租书方式比较划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
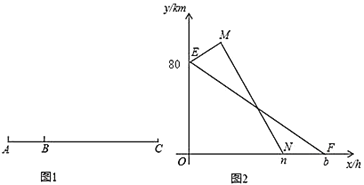
【题目】如图有A、B、C三地依次在一条笔直的公路上,A、B两地相距40km,一辆甲车以40km/h的速度从B地到C地;同时一辆乙车以80km/h的速度从B地开往A地,到达A地后,然后以120km/h的速度开往C地,两车在各段内均匀速行驶,图中线段EF与折线EMN分别表示甲、乙两车距C地的路程y(千米)与行驶时间x(小时)之间的函数关系图象.
(1)写出点M的坐标为_______;点E的纵坐标的意义是________.
(2)请直接写出n,b的值,并求出线段EF与MN的函数关系式;
(3)两车出发几小时后,乙车追上甲车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长为8cm,宽为6cm的矩形纸片上,现要剪下一个腰长为5cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上).则剪下的等腰三角形的面积为______cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰三角形CDE,其中∠DCE=90°,连接BE.
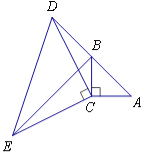
(1)求证:△ACD≌△BCE;
(2)若AB=3cm,则BE= cm;
(3)BE与AD有何位置关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
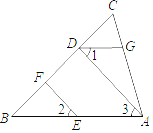
【题目】填写下列空格完成证明:如图, EF∥AD , 1 2 , BAC 70 ,求AGD .
解:∵ EF∥AD ,
∴ 2 .( )
∵ 1 2 ,
∴ 1 3.( )
∴ ∥ .( )
∴ BAC 180 .( )
∵ BAC 70 ,
∴ AGD .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com