
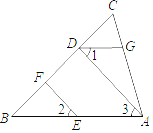
【题目】填写下列空格完成证明:如图, EF∥AD , 1 2 , BAC 70 ,求AGD .
解:∵ EF∥AD ,
∴ 2 .( )
∵ 1 2 ,
∴ 1 3.( )
∴ ∥ .( )
∴ BAC 180 .( )
∵ BAC 70 ,
∴ AGD .
【答案】∠3 ;两直线平行,同位角相等;等量代换;DG∥AB ;内错角相等,两直线平行;∠AGD ;两直线平行,同旁内角互补;110.
【解析】
此题要注意由EF∥AD,可得∠2=∠3,由等量代换可得∠1=∠3,可得DG∥BA,根据平行线的性质可得∠BAC+∠AGD=180°,即可求解.
∵EF=AD,
∴∠2=∠3,(两直线平行,同位角相等)
∵∠1=∠2,
∴∠1=∠3,(等量代换)
∴DG∥AB(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
∵∠BAC=70°,
∴∠AGD=110°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG;AB;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110.


 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】永嘉某商店试销一种新型节能灯,每盏节能灯进价为18元,试销过程中发现,每周销量y(盏)与销售单价x(元)之间关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣进价)
(1)写出每周的利润w(元)与销售单价x(元)之间函数解析式;
(2)当销售单价定为多少元时,这种节能灯每周能够获得最大利润?最大利润是多少元?
(3)物价部门规定,这种节能灯的销售单价不得高于30元.若商店想要这种节能灯每周获得350元的利润,则销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
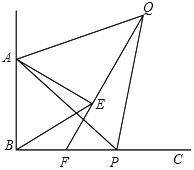
【题目】如图,![]() ,P为射线BC上任意一点
,P为射线BC上任意一点![]() 点P和点B不重合
点P和点B不重合![]() ,分别以AB,AP为边在
,分别以AB,AP为边在![]() 内部作等边
内部作等边![]() 和等边
和等边![]() ,连结QE并延长交BP于点F,连接EP,若
,连结QE并延长交BP于点F,连接EP,若![]() ,
,![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)12016 +![]() 3.14 π 0
3.14 π 0
(2) 3a2 3 2a a5
(3) x 2 x 1 3xx 1
(4)2a b c2a b c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作EFGD,连结BG,分别交EF和DC于点M,N,则 ![]() = .
= . 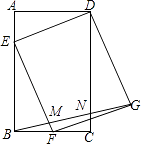
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题
(1)【问题提出】如图1.△ABC是等边三角形,点D在线段AB上.点E在直线BC上.且∠DEC=∠DCE.求证:BE=AD;
(2)【类比学习】如图2.将条件“点D在线段AB上”改为“点D在线段AB的延长线上”,其他条件不变.判断线段AB,BE,BD之间的数量关系,并说明理由.
(3)【扩展探究】如图3.△ABC是等腰三角形,AB=AC,∠BAC=120°,点D在线段AB的反向延长线上,点E在直线BC上,且∠DEC=∠DCE,【类比学习】中的线段AB、BE、BD之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出线段AB,BE,BD之间的数量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1 是一个长为 4a、宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图 2).
(1)图 2 中的阴影部分的面积为 ;(用 a、b 的代数式表示)
(2)观察图 2 请你写出a b2 、a b2 、ab 之间的等量关系是 ;
(3)根据⑵中的结论,若 x y 5 , x y ![]() ,则 x y2 =_______.
,则 x y2 =_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com