
【题目】已知二次函数y=ax2+bx+c的图象如图所示,OA=OC,则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式:①![]() =﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )
=﹣1;②ac+b+1=0;③abc>0;④a﹣b+c>0.其中正确的个数是( )
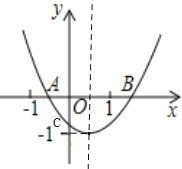
A. 4个 B. 3个 C. 2个 D. 1个
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
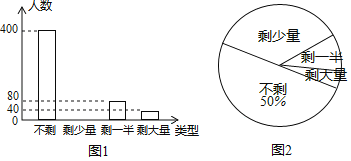
【题目】某企业工会开展“一周工作量完成情况”调查活动,随机调查了部分员工一周的工作量剩余情况,并将调查结果统计后绘制成如图1和图2所示的不完整统计图.
(1)被调查员工人数为 人:
(2)把条形统计图补充完整;
(3)若该企业有员工10000人,请估计该企业某周的工作量完成情况为“剩少量”的员工有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=![]() ,∠B=
,∠B=![]() ,AC=1,BC=
,AC=1,BC=![]() ,AB=2,AC在直线l上,将△ABC绕点A顺时针转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+
,AB=2,AC在直线l上,将△ABC绕点A顺时针转到位置①可得到点P1,此时AP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=3+![]() …,按此顺序继续旋转,得到点P2016,则AP2016=( )
…,按此顺序继续旋转,得到点P2016,则AP2016=( )
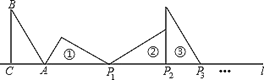
A. 2016+671![]() B. 2016+672
B. 2016+672![]()
C. 2017+671![]() D. 2017+672
D. 2017+672![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠BAC=45°.
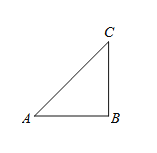
(1)尺规作图:
①在CA的延长线上截取AD=AB,并连结BD;
②在∠BAC内部作∠CAE=∠ABD,交BC边于点E;(保留作图痕迹,不写作法)
(2)求∠AEC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )
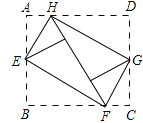
A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国七十周年,南岗区准备对某道路工程进行改造,若请甲工程队单独做此工程需4个月完成,若请乙工程队单独做此工程需6个月完成,若甲、乙两队合作2个月后,甲工程队到期撤离,则乙工程队再单独需几个月能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3).
(Ⅰ)求△ABC的面积;
(Ⅱ)在图中作出△ABC关于![]() 轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.
轴的对称图形△A1B1C1,并写出点A1、B1、C1的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=x+3分别交x轴、y轴于A,C两点,抛物线y=ax2+bx+c(a≠0),经过A,C两点,与x轴交于点B(1,0).
(1)求抛物线的解析式;
(2)点D为直线AC上一点,点E为抛物线上一点,且D,E两点的横坐标都为2,点F为x轴上的点,若四边形ADEF是平行四边形,请直接写出点F的坐标;
(3)若点P是线段AC上的一个动点,过点P作x轴的垂线,交抛物线于点Q,连接AQ,CQ,求△ACQ的面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com