
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
下面,我们通过折叠的方式折出一个![]() 矩形,如图a所示.
矩形,如图a所示.
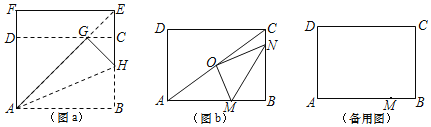
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为![]() 矩形.
矩形.
(1)证明:四边形ABCD为![]() 矩形;
矩形;
(2)点M是边AB上一动点.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求![]() 的值;
的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2![]() ,则DR的最小值= .
,则DR的最小值= .
【答案】(1)见解析;(2)![]() ,2.
,2.
【解析】
(1)先判断出∠DAG=45°,进而判断出四边形ABCD是矩形,再求出AB:AD的值,即可得出结论;
(2)①如图b,先判断出四边形BQOP是矩形,进而得出![]() ,再判断出Rt△QON∽Rt△POM,进而判断出
,再判断出Rt△QON∽Rt△POM,进而判断出![]() ,即可得出结论;
,即可得出结论;
②作M关于直线BC对称的点P,则△DMN的周长最小,判断出![]() ,得出AB=CD=
,得出AB=CD=![]() a.进而得出BP=BM=AB-AM=(
a.进而得出BP=BM=AB-AM=(![]() -1)a.即可得出结论;
-1)a.即可得出结论;
③先求出BC=AD=2,再判断出点R是BC为直径的圆上,即可得出结论.
证明:(1)设正方形ABEF的边长为a,
∵AE是正方形ABEF的对角线,
∴∠DAG=45°,
由折叠性质可知AG=AB=a,∠FDC=∠ADC=90°,
则四边形ABCD为矩形,
∴△ADG是等腰直角三角形.
∴![]() ,
,
∴![]() .
.
∴四边形ABCD为![]() 矩形;
矩形;
(2)①解:如图,作OP⊥AB,OQ⊥BC,垂足分别为P,Q.
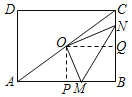
∵四边形ABCD是矩形,∠B=90°,
∴四边形BQOP是矩形.
∴∠POQ=90°,OP∥BC,OQ∥AB.
∴![]() .
.
∵O为AC中点,
∴OP=![]() BC,OQ=
BC,OQ=![]() AB.
AB.
∵∠MON=90°,
∴∠QON=∠POM.
∴Rt△QON∽Rt△POM.
∴![]() .
.
∴![]() .
.
②解:如图c,作M关于直线BC对称的点P,连接DP交BC于点N,连接MN.则△DMN的周长最小,
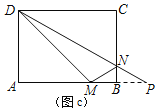
∵DC∥AP,
∴![]() ,
,
设AM=AD=a,则AB=CD=![]() a.
a.
∴BP=BM=AB-AM=(![]() -1)a.
-1)a.
∴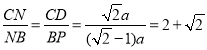 ,
,
③如备用图,
∵四边形ABCD为![]() 矩形,AB=2
矩形,AB=2![]() ,
,
∴BC=AD=2,
∵BR⊥CM,
∴点R在以BC为直径的圆上,记BC的中点为I,
∴CI=![]() BC=1,
BC=1,
∴DR最小=![]() -1=2
-1=2
故答案为:2


科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年我国“十二五”规划圆满完成,“十三五”规划顺利实施,经济社会发展取得历史性成就,发生历史性变革.这五年来,经济实力跃上新台阶,国内生产总值达到82.7万亿元,2018年,我国国内生产总值达到900309亿元人民币,首次迈过90万亿元门槛,比上一年同比增长66%,实现了65%左右的预期发展目标.下面的统计图反映了我国2013年到2018年国内生产总值及其增长速度情况,其中国内生产总值绝对数按现价计算,增长速度按不变价格计算
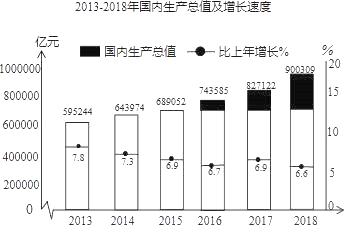
根据以上信息,回答下列问题
(1)把统计图补充完整;
(2)我国2013年到2018年这六年的国内生产总值增长速度的中位数是 %;
(3)2019年政府工作报告提出,今年的预期目标是国内生产总值比2018年增长6‰﹣6.5%,通过计算说明2019年我国国内生产总值至少达到多少亿元,即可达到预期目标.
查看答案和解析>>
科目:初中数学 来源: 题型:
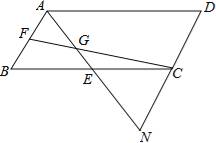
【题目】如图,在ABCD中,E,F分别为BC,AB中点,连接FC,AE,且AE与FC交于点G,AE的延长线与DC的延长线交于点N.
(1)求证:△ABE≌△NCE;
(2)若AB=3n,FB=![]() GE,试用含n的式子表示线段AN的长.
GE,试用含n的式子表示线段AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
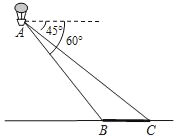
【题目】如图,小明在热气球A上看到正前方横跨河流两岸的大桥BC,测得B,C两点的俯角分别为60°和45°,已知热气球离地面的高度为120m,且大桥与地面在同一水平面上,求大桥BC的长度(结果保留整数,![]() ≈1.72).
≈1.72).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校要开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
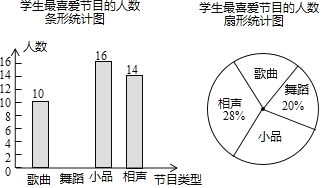
请你根据图中信息,回答下列问题:
(1)本次共调查了 名学生.
(2)在扇形统计图中,“歌曲”所在扇形的圆心角等于 度.
(3)补全条形统计图(标注频数).
(4)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为 人.
(5)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①② B. ①③ C. ①②③ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
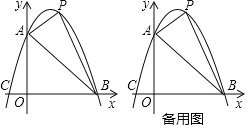
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(-2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了维护国家主权和海洋权利,我国海监部门对中国海域实现常态化管理.某日,我国海监船在某海岛附近的海域执行巡逻任务.如图,此时海监船位于海岛P的北偏东30°方向,距离海岛100海里的A处,它沿正南方向航行一段时间后,到达位于海岛P的南偏东45°方向的B处,求海监船航行了多少海里(结果保留根号)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com