
【题目】2017年我国“十二五”规划圆满完成,“十三五”规划顺利实施,经济社会发展取得历史性成就,发生历史性变革.这五年来,经济实力跃上新台阶,国内生产总值达到82.7万亿元,2018年,我国国内生产总值达到900309亿元人民币,首次迈过90万亿元门槛,比上一年同比增长66%,实现了65%左右的预期发展目标.下面的统计图反映了我国2013年到2018年国内生产总值及其增长速度情况,其中国内生产总值绝对数按现价计算,增长速度按不变价格计算
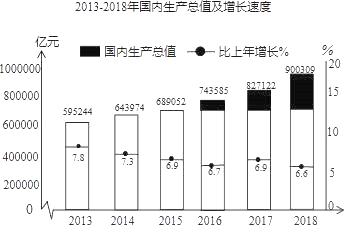
根据以上信息,回答下列问题
(1)把统计图补充完整;
(2)我国2013年到2018年这六年的国内生产总值增长速度的中位数是 %;
(3)2019年政府工作报告提出,今年的预期目标是国内生产总值比2018年增长6‰﹣6.5%,通过计算说明2019年我国国内生产总值至少达到多少亿元,即可达到预期目标.
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点D,点E是直线AC上一动点,连接DE,过点D作
于点D,点E是直线AC上一动点,连接DE,过点D作![]() ,交直线BC于点F.
,交直线BC于点F.
![]() 探究发现:
探究发现:
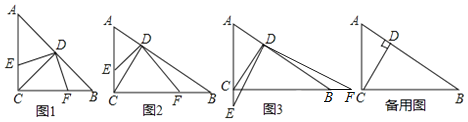
如图1,若![]() ,点E在线段AC上,则
,点E在线段AC上,则![]() ______;
______;
![]() 数学思考:
数学思考:
![]() 如图2,若点E在线段AC上,则
如图2,若点E在线段AC上,则![]() ______
______![]() 用含m,n的代数式表示
用含m,n的代数式表示![]() ;
;
![]() 当点E在直线AC上运动时,
当点E在直线AC上运动时,![]() 中的结论是否任然成立?请仅就图3的情形给出证明;
中的结论是否任然成立?请仅就图3的情形给出证明;
![]() 拓展应用:若
拓展应用:若![]() ,
,![]() ,
,![]() ,请直接写出CE的长.
,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形OABC的边OC、OA分别在x、y轴的正半轴上,设点B(4,4),点P(t,0)是x轴上一动点,过点O作OH⊥AP于点H,直线OH交直线BC于点D,连AD.
(1)如图1,当点P在线段OC上时,求证:OP=CD;
(2)在点P运动过程中,△AOP与以A、B、D为顶点的三角形相似时,求t的值;
(3)如图2,抛物线y=﹣![]() x2+
x2+![]() x+4上是否存在点Q,使得以P、D、Q、C为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
x+4上是否存在点Q,使得以P、D、Q、C为顶点的四边形为平行四边形?若存在,请求出t的值;若不存在,请说明理由.
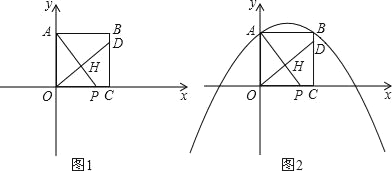
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)
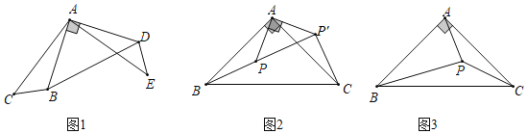
(1)如图1,将△ABC绕点A逆时针旋转90°得到△ADE,连接BD,则∠ABD的度数是______.
(类比探究)
(2)如图2,在等腰直角三角形ABC内取一点P,使∠APB=135°,将△ABP绕顶点A逆时针旋转90°得到△ACP',连接PP'.请猜想BP与CP'有怎样的位置关系,并说明理由.
(解决问题)
(3)如图3,在等腰直角三角形ABC内任取一点P,连接PA、PB、PC.求证:PC+![]() PA>PB.
PA>PB.
查看答案和解析>>
科目:初中数学 来源: 题型:
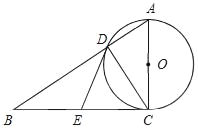
【题目】如图,在Rt△ABC中,∠ACB=90°,E是BC的中点,以AC为直径的⊙O与AB边交于点D,连接DE.
(1)求证:DE是⊙O的切线;
(2)若CD=6cm,DE=5cm,求⊙O直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
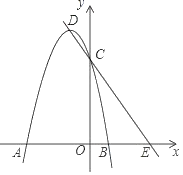
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2ax﹣3a(a<0)与x轴相交于A、B两点与y轴相交于点C,顶点为D,直线DC与x轴相交于点E.
(1)当a=﹣1时,抛物线顶点D的坐标为 ,OE= ;
(2)OE的长是否与a值有关,说明你的理由;
(3)设∠DEO=β,当β从30°增加到60°的过程中,点D运动的路径长;
(4)以DE为斜边,在直线DE的右上方作等腰Rt△PDE.设P(m,n),请直接写出n关于m的函数解析式及自变量m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:长宽比为![]() :1(n为正整数)的矩形称为
:1(n为正整数)的矩形称为![]() 矩形.
矩形.
下面,我们通过折叠的方式折出一个![]() 矩形,如图a所示.
矩形,如图a所示.
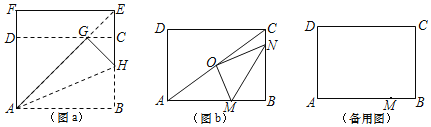
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF,BE上,折痕为CD.则四边形ABCD为![]() 矩形.
矩形.
(1)证明:四边形ABCD为![]() 矩形;
矩形;
(2)点M是边AB上一动点.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②若AM=AD,点N在边BC上,当△DMN的周长最小时,求![]() 的值;
的值;
③连接CM,作BR⊥CM,垂足为R.若AB=2![]() ,则DR的最小值= .
,则DR的最小值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解八年级学生双休日的课外阅读情况,学校随机调查了该年级25名学生,得到了一组样本数据,其统计表如下:
八年级25名学生双休日课外阅读时间统计表
阅读时间 | 1小时 | 2小时 | 3小时 | 4小时 | 5小时 | 6小时 |
人数 | 3 | 4 | 6 | 3 | 2 |
(1)请求出阅读时间为4小时的人数所占百分比;
(2)试确定这个样本的众数和平均数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com