
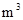 时,按2元/
时,按2元/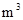 计费;月用水量超过20
计费;月用水量超过20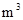 时,其中的20
时,其中的20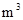 仍按2元/
仍按2元/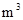 收费,超过部分按
收费,超过部分按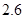 元/
元/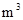 计费.设每户家庭用用水量为
计费.设每户家庭用用水量为 时,应交水费
时,应交水费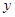 元.
元.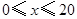 和
和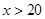 时
时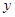 与
与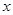 的函数表达式;
的函数表达式;| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 42.6元 |
科目:初中数学 来源:不详 题型:解答题
| 物品重量(千克) | 支付费用(元) |
| 18 | 39 |
| 25 | 53 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 .动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为( )
.动点P从点B出发,沿梯形的边由B→C→D→A运动.设点P运动的路程为x,△ABP的面积为y.把y看作x的函数,函数的图像如图乙所示,则△ABC的面积为( ) 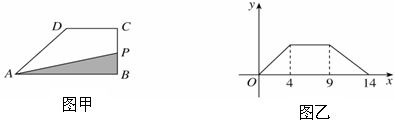
| A.10 | B.16 | C.18 | D.32 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸
,公路两侧是平坦的草地.在数学活动课上,老师要求测量河对岸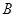 点到公路的距离,请你设计一个测量方案.要求:
点到公路的距离,请你设计一个测量方案.要求:
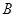 点到公路的距离.
点到公路的距离.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 相乘:
相乘: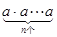 记为
记为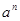 。如23=8,此时,3叫做以2为底8的对数,记为
。如23=8,此时,3叫做以2为底8的对数,记为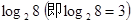 。
。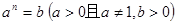 ,则n叫做以
,则n叫做以 为底b的对数,记为
为底b的对数,记为 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为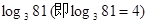 。
。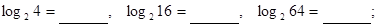
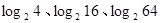 之间又满足怎样的关系式?
之间又满足怎样的关系式? 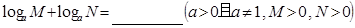
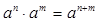 以及对数的含义证明上述结论。
以及对数的含义证明上述结论。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
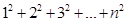 .但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道
.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道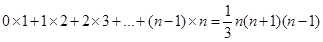 时,我们可以这样做:
时,我们可以这样做: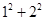 =(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)
=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)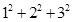 =(1+0)×1+(1+1)×2+(l+2)×3
=(1+0)×1+(1+1)×2+(l+2)×3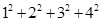 =(1+0)×1+(1+1)×2+(l+2)×3+(1+3)×4;
=(1+0)×1+(1+1)×2+(l+2)×3+(1+3)×4;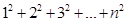 =(1+0)×1+(1+1)×2+(1+2)×3+…[(1+(n-l)]n
=(1+0)×1+(1+1)×2+(1+2)×3+…[(1+(n-l)]n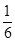 ×(___________)
×(___________)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com