
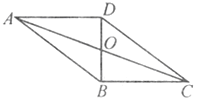
【题目】如图,四边形ABCD是平行四边形,AD⊥BD,AD=8,AB=10,OB,AC的长及□ABCD的面积.
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论: ⑴b2﹣4ac>0;
⑵2a=b;
⑶点(﹣ ![]() ,y1)、(﹣
,y1)、(﹣ ![]() ,y2)、(
,y2)、( ![]() ,y3)是该抛物线上的点,则y1<y2<y3;
,y3)是该抛物线上的点,则y1<y2<y3;
⑷3b+2c<0;
⑸t(at+b)≤a﹣b(t为任意实数).
其中正确结论的个数是( )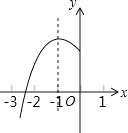
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
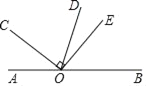
【题目】如图,点O是直线AB上一点,OD平分∠BOC,∠COE=90°
(1)若∠AOC=40°,求∠BOE和∠DOE的度数;
(2)若∠AOC=α,求∠DOE的度数(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
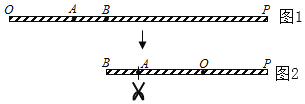
【题目】如图1,OP为一条拉直的细线,长为7cm,A,B两点在OP上,若先握住点B,将OB折向BP,使得OB重叠在BP上,如图![]() 再从图2的A点及与A点重叠处一起剪开,使得细线分成三段
再从图2的A点及与A点重叠处一起剪开,使得细线分成三段![]() 若这三段的长度由短到长之比为1:2:4,其中以点P为一端的那段细线最长,则OB的长为______cm.
若这三段的长度由短到长之比为1:2:4,其中以点P为一端的那段细线最长,则OB的长为______cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1).
(1)请根据图1,回答下列问题:
①这个班共有名学生,发言次数是5次的男生有人、女生有人;
②男、女生发言次数的中位数分别是次和次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数和全班增加的发言总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况如图所示:根据条形图提供的信息,下列说法中,正确的是( )
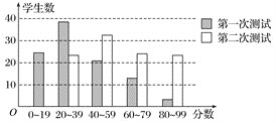
A. 两次测试,最低分在第二次测试中
B. 第一次测试和第二次测试的平均分相同
C. 第一次分数的中位数在20~39分数段
D. 第二次分数的中位数在60~79分数段
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,D是BC边上的一点,连接AD,取AD的中点E,过点A作BC的平行线与CE的延长线交于点F,连接DF.
(1)求证:AF=DC;
(2)请问:AD与CF满足什么条件时,四边形AFDC是矩形,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com