
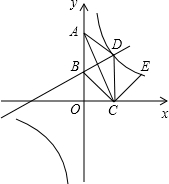
 ��ͼ����ƽ��ֱ������ϵ�У�����ABCD�ı�AB��y����������ϣ���C��x���ϣ���D�ڵ�һ���ޣ�ֱ��y=$\frac{1}{2}$x+3������B�͵�D��˫����y=$\frac{k}{x}$��k��0��Ҳ������D��
��ͼ����ƽ��ֱ������ϵ�У�����ABCD�ı�AB��y����������ϣ���C��x���ϣ���D�ڵ�һ���ޣ�ֱ��y=$\frac{1}{2}$x+3������B�͵�D��˫����y=$\frac{k}{x}$��k��0��Ҳ������D������ ��1����ֱ��BD�Ľ���ʽ��x=0���yֵ�����ɵó�OB�ij�����OC=x����D��x��$\frac{1}{2}$x+3����C��x��0�����������ε����ʽ�Ϲ��ɶ������ɵó�����x�ķ��̣��ⷽ�̼������OC�ij��ȣ�
��2���ɹ��ɶ������BC�ij��ȣ����OB��OC���ɵó���A��B��C�����꣬�ٸ������ε����ʼ��ɵó���D�����꣬�ɵ�D���������÷���������ͼ���ϵ�������������������������������ʽ�����E������Ϊ��n��$\frac{20}{n}$����n��0�����������ε������ʽ�������ε������ʽ�Լ���ECD�������������ABCD�����$\frac{1}{4}$�����ɵó�����n�ĺ�����ֵ���ŵ�һԪһ�η��̣��ⷽ�����nֵ����������E�����м��ɵó����ۣ�
��3�������߶�BCΪ�ߺ����߶�BCΪ�Խ�������鿼�ǣ���ÿ��������ٷֵ�P��x���Ϻ���y���Ͽ��ǣ������P�����꣬��ϵ�B��C��P�����꼴�ɵó���Q�����꣬�ɵ�Q�ڷ����������ϼ��������P��Q�����꣬�ɵ�Q���������ô���ϵ�����������ֱ��OQ�Ľ���ʽ��
��� �⣺��1����y=$\frac{1}{2}$x+3��x=0����y=3��
��OB=3��
��OC=x����D��x��$\frac{1}{2}$x+3����C��x��0����
���ı���ABCDΪ���Σ�
��CD=$\frac{1}{2}$x+3=BC=$\sqrt{{x}^{2}+{3}^{2}}$��
��ã�x=4��x=0����ȥ����
�ʴ�Ϊ��3��4��
��2����BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=5��
��A��0��8����
�֡�C��4��0����B��0��3����
��D��4��5����
��5=$\frac{k}{4}$��k=20��
�෴������������ʽΪy=$\frac{20}{x}$��
���E��������n��$\frac{20}{n}$����n��0����
S��ECD=$\frac{1}{2}$CD•|xE-xC|=$\frac{5}{2}$|n-4|��S����ABCD=AB•OC=20��
��S��ECD=$\frac{1}{4}$S����ABCD=5����|n-4|=2��
��ã�n=2��n=6��
���E��������2��10����6��$\frac{10}{3}$����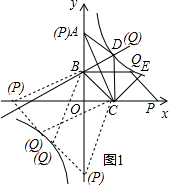
��3����B��C��P��QΪ������ı�����ƽ���ı��η����������
�����߶�BCΪ�ߣ���ͼ1��ʾ��
����P��x����ʱ�����P������Ϊ��m��0����
��B��0��3����C��4��0����
��Q��m-4��3����m+4��-3����
��3=$\frac{20}{m-4}$��-3=$\frac{20}{m+4}$��
��ã�m=$\frac{32}{3}$��m=-$\frac{32}{3}$��
��ʱ��Q��$\frac{20}{3}$��3����-$\frac{20}{3}$��-3����
����P��y���ϣ���ʱP��A�غϣ�D��Q�غϣ�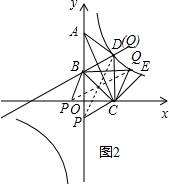
�ɶԳ��Կɵó���Q��4��5����-4��-5����
�����߶�BCΪ�Խ��ߣ���ͼ2��ʾ��
����P��x����ʱ����P��m��0����
��B��0��3����C��4��0����
��Q��2-m��3����
��3=$\frac{20}{2-m}$����ã�m=-$\frac{14}{3}$��
��ʱ��Q��$\frac{20}{3}$��3����
����P��y����ʱ����ʱ��Q��D�غϣ�
��Q��4��5����
���Ͽ�֪����Q������Ϊ��$\frac{20}{3}$��3������-$\frac{20}{3}$��-3������4��5����-4��-5����
��ֱ��OQ�Ľ���ʽΪy=ax��
��Q��Ϊ��$\frac{20}{3}$��3���ͣ�-$\frac{20}{3}$��-3��ʱ����3=$\frac{20}{3}$a����ã�a=$\frac{9}{20}$��
��ʱOQ�Ľ���ʽΪy=$\frac{9}{20}$x��
��Q��Ϊ��4��5���ͣ�-4��-5��ʱ����5=4a����ã�a=$\frac{5}{4}$��
��ʱOQ�Ľ���ʽΪy=$\frac{5}{4}$x��
��ֱ��OQ�Ľ���ʽΪy=$\frac{9}{20}$x��y=$\frac{5}{4}$x��
���� ���⿼����һ�κ���ͼ���ϵ���������������ε����ʡ����ɶ����Լ�����ϵ������������ʽ������Ĺؼ��ǣ���1���������ε����ʽ�Ϲ��ɶ������OC����2���е�D���������÷���������ͼ���ϵ������������������������Ľ���ʽ����3����������ǣ����������е��⣬��3���ѶȲ��������ʱ���Ȱ����߶�BCΪ�ߺ����߶�BCΪ�Խ��������������ǣ��ٰ���P��x��y���Ϸ֣������������Ŀʱ�벻��ͼ�Σ��������ν�Ͻ�������Ǹ��ʵĹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | M��N | B�� | M��N | C�� | M=N | D�� | M��N |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�����ı���ABCD�DZ߳�Ϊ4�������Σ���E�ڱ�BC�ϣ������B����C�غϣ�����AEF=90�㣬��EF����������ǵ�ƽ�����ڵ�F��AF��CD�ཻ�ڵ�H�����н��ۣ��١�BAE=��FEC����AE=EF���ۡ�CEF��������ֵΪ2����BE+DH=EH��������ȷ���۵ĸ����ǣ�������
��ͼ�����ı���ABCD�DZ߳�Ϊ4�������Σ���E�ڱ�BC�ϣ������B����C�غϣ�����AEF=90�㣬��EF����������ǵ�ƽ�����ڵ�F��AF��CD�ཻ�ڵ�H�����н��ۣ��١�BAE=��FEC����AE=EF���ۡ�CEF��������ֵΪ2����BE+DH=EH��������ȷ���۵ĸ����ǣ�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���AOB�DZ߳�Ϊ2�ĵȱ������Σ�ֱ��L��x���ڵ�C��2��0��������AB��E���ҡ�ADE���COD�������ȣ���E��˫����y=$\frac{k}{x}$��x��0���ϣ���k=-$\frac{3\sqrt{3}}{4}$��
��ͼ����ƽ��ֱ������ϵ�У���AOB�DZ߳�Ϊ2�ĵȱ������Σ�ֱ��L��x���ڵ�C��2��0��������AB��E���ҡ�ADE���COD�������ȣ���E��˫����y=$\frac{k}{x}$��x��0���ϣ���k=-$\frac{3\sqrt{3}}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �ھ���ABCD�У�AB=3��BC=4��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ����������У��ٶȾ�Ϊ1cm/s���˶�ʱ��Ϊt�룬0��t��5��
�ھ���ABCD�У�AB=3��BC=4��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ����������У��ٶȾ�Ϊ1cm/s���˶�ʱ��Ϊt�룬0��t��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �Ķ����ϣ�
�Ķ����ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
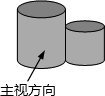 ��ͼ��ʾ��������������������һ���Բ������ɣ�С����������������ͼ����ô������������ͼ�е�����ͼӦ���ǣ�������
��ͼ��ʾ��������������������һ���Բ������ɣ�С����������������ͼ����ô������������ͼ�е�����ͼӦ���ǣ�������| A�� | 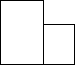 | B�� |  | C�� | 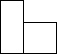 | D�� |  |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com