
 阅读材料:
阅读材料:分析 (1)首先分别求出d(P1,l1)、d(l1,l2)、d(P2,l2)的值各是多少,再把它们求和,求出d(P1,P2|l1,l2)的值是多少即可.
(2)①首先作P1A⊥l3于点A,P2B⊥l3于点B,连接P1P2交l3于点C,然后根据P1A+P2B≤P1P2,可得当P1P2⊥l3时,P1A+P2B的值最大,据此求出k的值是多少即可.
②首先作P1A⊥l3于点A,P2B⊥l3于点B,P1、P3关于原点对称,P3C⊥l3于点C,P2P3交l3于点D,然后根据P2B+P3C≤P2P3,可得当P2P3⊥l3时,P2B+P3C取到最大值,据此求出k的值是多少即可.
解答 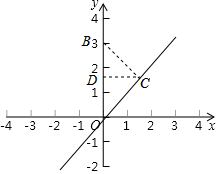 解:(1)∵P1(4,0),P2(0,3),l1:y=x,l2:y=$\sqrt{3}$x,
解:(1)∵P1(4,0),P2(0,3),l1:y=x,l2:y=$\sqrt{3}$x,
如图,过点A作AB⊥l2,
∵y=$\sqrt{3}$x,
∴∠BOC=30°,
∴∠OBC=60°,
设CD=x,则OD=$\sqrt{3}$x,BD=$\frac{\sqrt{3}}{3}$CD=$\frac{\sqrt{3}}{3}$x,
∵OB=3,
∴x=$\frac{3\sqrt{3}}{4}$,
∴BC=2BD=$\frac{3}{2}$,
∴d(P1,P2|l1,l2)=d(P1,l1)+d(l1,l2)+d(P2,l2)
=$\frac{4}{\sqrt{2}}$+0+$\frac{3}{2}$
=2$\sqrt{2}$+$\frac{3}{2}$;
故答案为:2$\sqrt{2}$+$\frac{3}{2}$;
(2)①如图1,作P1A⊥l3于点A,P2B⊥l3于点B,连接P1P2交l3于点C,
d(P1,P2|l3,l3)=d(P1,l3)+d(l3,l3)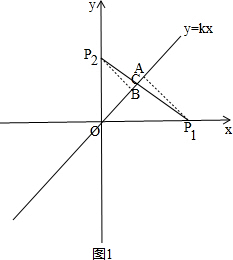 +d(P2,l3)=P1A+P2B,
+d(P2,l3)=P1A+P2B,
∵P1A≤P1C,P2B≤P2C,
∴P1A+P2B≤P1P2,
∴当P1P2⊥l3时,
P1A+P2B的最大值是:$\sqrt{O{P}_{1}^{2}+O{P}_{2}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
此时k=tan∠OP2P1=$\frac{O{P}_{1}}{O{P}_{2}}$=$\frac{4}{3}$,
∴若k>0,当d(P1,P2|l3,l3)最大时,k=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$;
②如图2,作P1A⊥l3于点A,P2B⊥l3于点B,P1、P3关于原点对称,P3C⊥l3于点C,P2P3交l3于点D,
∵P1、P3关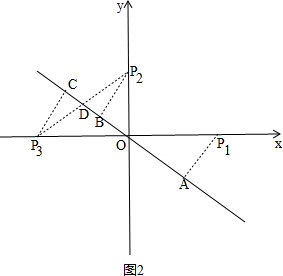 于原点对称,
于原点对称,
∴P1A=P3C,
∴d(P1,P2|l3,l3)=d(P1,l3)+d(l3,l3)+d(P2,l3)=P1A+P2B=P2B+P3C,
∵P2B≤P2D,P3C≤P3D,
∴P2B+P3C≤P2P3,
∴当P2P3⊥l3时,
P2B+P3C的最大值是:$\sqrt{O{P}_{3}^{2}+O{P}_{2}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
此时k=-tan∠OP2P3=-$\frac{O{P}_{3}}{O{P}_{2}}$=-$\frac{4}{3}$,
∴若k<0,当d(P1,P2|l3,l3)最大时,k=-$\frac{4}{3}$.
点评 此题属于一次函数的综合题.考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.解答此题的关键是理解d(P1,P2|l1,l2)=d(P1,l1)+d(l1,l2)+d(P2,l2)的意义和求法.


科目:初中数学 来源: 题型:填空题
| 项目 | 着装 | 队形 | 精神风貌 |
| 成绩(分) | 90 | 94 | 92 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
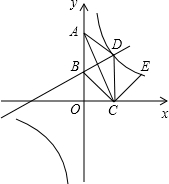 如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.
如图,在平面直角坐标系中,菱形ABCD的边AB在y轴的正半轴上,点C在x轴上,点D在第一象限.直线y=$\frac{1}{2}$x+3经过点B和点D.双曲线y=$\frac{k}{x}$(k≠0)也经过点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.
如图,菱形ABCD中,∠A=60°,边长为4厘米,动点P从A出发,以1厘米/秒的速度沿A-B-C运动,在P出发1秒后,点Q以同样的速度沿相同的路线运动,过点P、Q的直线L1、L2相互平行,且都与AB边所在的直线成60°角,设P点运动的时间为x秒(1<x<8),直线L1、L2在菱形ABCD上截得的图形面积为y平方厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com